已知數列{an}前n項的和為Sn,前n項的積為Tn,且滿足Tn=2n(1-n).
①求a1;
②求證:數列{an}是等比數列;
③是否存在常數a,使得(Sn+1-a)2=(Sn+2-a)(Sn-a)對n∈N+都成立?若存在,求出a,若不存在,說明理由.
【答案】
分析:(1)由“數列{a
n}前n項的和為S
n,前n項的積為T
n,且滿足T
n=2
n(1-n)”令n=1可求解.
(2)證明:由T
n=2
n(1-n)解得T
(n-1)=2
(n-1)(2-n)兩式相除,整理可得數列{a
n}是等比數列;
(3)由(2)求解得
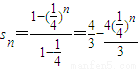
再求得
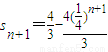
,
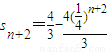
代入(S
n+1-a)
2=(S
n+2-a)(S
n-a)兩端驗證可即可.
解答:解:(1)∵數列{a
n}前n項的和為S
n,前n項的積為T
n,且滿足T
n=2
n(1-n).
∴a
1=T
1=2
1(1-1)=1
(2)證明:∵T
n=2
n(1-n).
∴T
(n-1)=2
(n-1)(2-n).
將上面兩式相除,
得:a
n=2
[-2(n-1)].
∴a
n=
 (n-1)
(n-1).
∵a
n+1=
 (n)
(n).
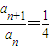
∴數列{a
n}是等比數列;
(3)∵
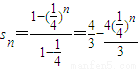
∴
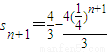
,
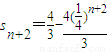
∵(S
n+1-a)
2=(S
n+2-a)(S
n-a)
∴(S
n+1-a)
2=
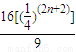
而:(S
n+2-a)(S
n-a)=(S
n+2-

)(S
n-

)=
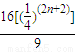
(S
n+1-

)
2=(S
n+2-

)(S
n-

)對n∈N
+都成立
即:存在常數a=

,使(S
n+1-a)
2=(S
n+2-a)(S
n-a)對n∈N
+都成立.
點評:本題主要考查數列的類型和數列的通項公式和前n項和公式,還考查了存在性問題,這類問題一般通過具體的探究出來,再證明.

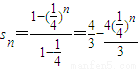 再求得
再求得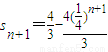 ,
,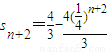
 (n-1).
(n-1). (n).
(n).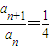
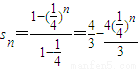
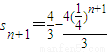 ,
,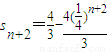
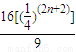
 )(Sn-
)(Sn- )=
)=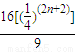
 )2=(Sn+2-
)2=(Sn+2- )(Sn-
)(Sn- )對n∈N+都成立
)對n∈N+都成立 ,使(Sn+1-a)2=(Sn+2-a)(Sn-a)對n∈N+都成立.
,使(Sn+1-a)2=(Sn+2-a)(Sn-a)對n∈N+都成立.
