
【題目】已知以![]() 為首項的數(shù)列
為首項的數(shù)列![]() 滿足:
滿足: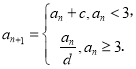
(1)當![]() ,
,![]() 時,求數(shù)列
時,求數(shù)列![]() 的通項公式;
的通項公式;
(2)當![]() ,
,![]() 時,試用
時,試用![]() 表示數(shù)列
表示數(shù)列![]() 前100項的和
前100項的和![]() ;
;
(3)當![]() (
(![]() 是正整數(shù)),
是正整數(shù)),![]() ,正整數(shù)
,正整數(shù)![]() 時,判斷數(shù)列
時,判斷數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 是否成等比數(shù)列?并說明理由.
是否成等比數(shù)列?并說明理由.
【答案】(1)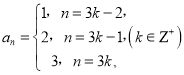 ;(2)
;(2)![]()
![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)根據(jù)遞推關系式先寫前幾項,再根據(jù)周期寫通項公式;
(2)根據(jù)遞推關系式先寫前幾項,再根據(jù)周期寫通項公式,最后根據(jù)分組求和以及等比數(shù)列求和公式得結(jié)果;
(3)分![]() 與
與![]() 兩種情況,根據(jù)遞推關系式確定
兩種情況,根據(jù)遞推關系式確定![]() ,
,![]() ,
,![]() ,再根據(jù)等比數(shù)列定義判斷
,再根據(jù)等比數(shù)列定義判斷
(1) 當![]() ,
,![]() 時,
時,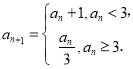
所以![]()
即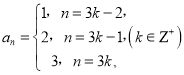 .
.
(2)當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,
(3)①當![]() 時,
時,![]() ;
;![]()
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
綜上所述,當![]() 時,數(shù)列
時,數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 是公比為
是公比為![]() 的等比數(shù)列.
的等比數(shù)列.
②當![]() 時,
時, ![]() ,
, ![]() ,
,
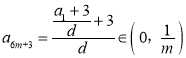 ,
,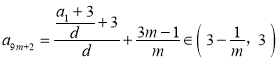 .
.
由于![]() ,
,![]() ,
,![]() ,
,
故數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 不是等比數(shù)列.
不是等比數(shù)列.
綜上,![]() 時數(shù)列
時數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 成等比數(shù)列;
成等比數(shù)列;
![]() 時數(shù)列
時數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 不成等比數(shù)列.
不成等比數(shù)列.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數(shù)學 來源: 題型:
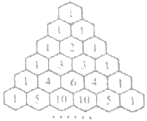
【題目】如圖所示,在“楊輝三角”中,去除所有為1的項,依次構成數(shù)列2,3,3,4,6,4,5,10,10,5,…,則此數(shù)列前21項的和為_______________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】大數(shù)據(jù)時代對于現(xiàn)代人的數(shù)據(jù)分析能力要求越來越高,數(shù)據(jù)擬合是一種把現(xiàn)有數(shù)據(jù)通過數(shù)學方法來代入某條數(shù)式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐標系上的一系列點,用函數(shù)
,n是平面直角坐標系上的一系列點,用函數(shù)![]() 來擬合該組數(shù)據(jù),盡可能使得函數(shù)圖象與點列
來擬合該組數(shù)據(jù),盡可能使得函數(shù)圖象與點列![]() 比較接近.其中一種描述接近程度的指標是函數(shù)的擬合誤差,擬合誤差越小越好,定義函數(shù)
比較接近.其中一種描述接近程度的指標是函數(shù)的擬合誤差,擬合誤差越小越好,定義函數(shù)![]() 的擬合誤差為:
的擬合誤差為:![]() .已知平面直角坐標系上5個點的坐標數(shù)據(jù)如表:
.已知平面直角坐標系上5個點的坐標數(shù)據(jù)如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函數(shù)
若用一次函數(shù)![]() 來擬合上述表格中的數(shù)據(jù),求該函數(shù)的擬合誤差
來擬合上述表格中的數(shù)據(jù),求該函數(shù)的擬合誤差![]() 的最小值,并求出此時的函數(shù)解析式
的最小值,并求出此時的函數(shù)解析式![]() ;
;
![]() 若用二次函數(shù)
若用二次函數(shù)![]() 來擬合題干表格中的數(shù)據(jù),求
來擬合題干表格中的數(shù)據(jù),求![]() ;
;
![]() 請比較第
請比較第![]() 問中的
問中的![]() 和第
和第![]() 問中的
問中的![]() ,用哪一個函數(shù)擬合題目中給出的數(shù)據(jù)更好?
,用哪一個函數(shù)擬合題目中給出的數(shù)據(jù)更好?![]() 請至少寫出三條理由
請至少寫出三條理由![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,且函數(shù)
,且函數(shù)![]() 為偶函數(shù)。
為偶函數(shù)。
(1)求![]() 的解析式;
的解析式;
(2)若方程![]() 有三個不同的實數(shù)根,求實數(shù)m的取值范圍。
有三個不同的實數(shù)根,求實數(shù)m的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,其中
,其中![]() 為自然對數(shù)的底數(shù),
為自然對數(shù)的底數(shù),![]() .
.
(1)求證:![]() ;
;
(2)若對于任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若存在![]() ,使
,使![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐O﹣ABCD中,底面ABCD四邊長為1的菱形,∠ABC=![]() ,OA⊥底面ABCD,OA=2,M為OA的中點,N為BC的中點.
,OA⊥底面ABCD,OA=2,M為OA的中點,N為BC的中點.
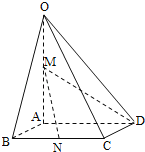
(1)證明:直線MN∥平面OCD;
(2)求異面直線AB與MD所成角的大小;
(3)求點B到平面OCD的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
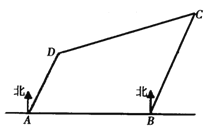
【題目】如圖,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正東方向,且與
的正東方向,且與![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏東
的北偏東![]() 方向,且與
方向,且與![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏東
的北偏東![]() 方向,且與
方向,且與![]() 相距
相距![]() ,一架飛機從城市
,一架飛機從城市![]() 出發(fā)以
出發(fā)以![]() 的速度向城市
的速度向城市![]() 飛行,飛行了
飛行,飛行了![]() ,接到命令改變航向,飛向城市
,接到命令改變航向,飛向城市![]() ,此時飛機距離城市
,此時飛機距離城市![]() 有( )
有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com