
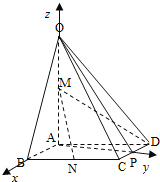
【題目】如圖,在四棱錐O﹣ABCD中,底面ABCD四邊長為1的菱形,∠ABC=![]() ,OA⊥底面ABCD,OA=2,M為OA的中點,N為BC的中點.
,OA⊥底面ABCD,OA=2,M為OA的中點,N為BC的中點.
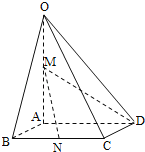
(1)證明:直線MN∥平面OCD;
(2)求異面直線AB與MD所成角的大小;
(3)求點B到平面OCD的距離.
【答案】(1) (2) ![]() .(3)
.(3) ![]()
【解析】
試題方法一:(1)取OB中點E,連接ME,NE,證明平面MNE∥平面OCD,方法是兩個平面內(nèi)相交直線互相平行得到,從而的到MN∥平面OCD;
(2)∵CD∥AB,∴∠MDC為異面直線AB與MD所成的角(或其補角)作AP⊥CD于P,連接MP
∵OA⊥平面ABCD,∴CD⊥MP菱形的對角相等得到∠ABC=∠ADC=![]() ,
,
利用菱形邊長等于1得到DP=![]() ,而MD利用勾股定理求得等于
,而MD利用勾股定理求得等于![]() ,在直角三角形中,利用三角函數(shù)定義求出即可.
,在直角三角形中,利用三角函數(shù)定義求出即可.
(3)AB∥平面OCD,∴點A和點B到平面OCD的距離相等,連接OP,過點A作AQ⊥OP于點Q,
∵AP⊥CD,OA⊥CD,∴CD⊥平面OAP,∴AQ⊥CD,
又∵AQ⊥OP,∴AQ⊥平面OCD,線段AQ的長就是點A到平面OCD的距離,求出距離可得.
方法二:(1)分別以AB,AP,AO所在直線為x,y,z軸建立坐標(biāo)系,分別表示出A,B,O,M,N的坐標(biāo),
求出![]() ,
,![]() ,
,![]() 的坐標(biāo)表示.設(shè)平面OCD的法向量為
的坐標(biāo)表示.設(shè)平面OCD的法向量為![]() =(x,y,z),則
=(x,y,z),則![]() ,
,
解得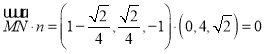 ,∴MN∥平面OCD
,∴MN∥平面OCD
(2)設(shè)AB與MD所成的角為θ,表示出![]() 和
和![]() ,利用a×b=|a||b|cosα求出叫即可.
,利用a×b=|a||b|cosα求出叫即可.
(3)設(shè)點B到平面OCD的距離為d,則d為![]() 在向量
在向量![]() 上的投影的絕對值,由
上的投影的絕對值,由![]()
![]()
得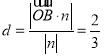 .所以點B到平面OCD的距離為
.所以點B到平面OCD的距離為![]() .
.
解:方法一(綜合法)
(1)取OB中點E,連接ME,NE
∵M(jìn)E∥AB,AB∥CD,∴ME∥CD
又∵NE∥OC,∴平面MNE∥平面OCD∴MN∥平面OCD
(2)∵CD∥AB,∴∠MDC為異面直線AB與MD所成的角(或其補角)
作AP⊥CD于P,連接MP
∵OA⊥平面ABCD,∴CD⊥MP
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]()
所以AB與MD所成角的大小為![]()
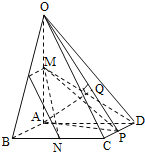
(3)∵AB∥平面OCD,
∴點A和點B到平面OCD的距離相等,連接OP,過點A作AQ⊥OP于點Q,
∵AP⊥CD,OA⊥CD,
∴CD⊥平面OAP,∴AQ⊥CD.
又∵AQ⊥OP,∴AQ⊥平面OCD,線段AQ的長就是點A到平面OCD的距離,
∵![]() ,
,![]() ,
,
∴ ,所以點B到平面OCD的距離為
,所以點B到平面OCD的距離為![]() .
.
方法二(向量法)![]()
作AP⊥CD于點P,如圖,分別以AB,AP,AO所在直線為x,y,z軸建立坐標(biāo)系:
A(0,0,0),B(1,0,0),![]() ,
,![]() ,
,
O(0,0,2),M(0,0,1),![]()
(1)![]() ,
,![]() ,
,![]()
設(shè)平面OCD的法向量為n=(x,y,z),則![]() ×
×![]() =0,
=0,![]() ×
×![]() =0
=0
即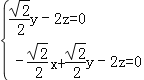
取![]() ,解得
,解得
∵![]() ×
×![]() =(
=(![]() ,
,![]() ,﹣1)×(0,4,
,﹣1)×(0,4,![]() )=0,
)=0,
∴MN∥平面OCD.
(2)設(shè)AB與MD所成的角為θ,
∵![]()
∴
∴![]() ,AB與MD所成角的大小為
,AB與MD所成角的大小為![]() .
.
(3)設(shè)點B到平面OCD的距離為d,則d為![]() 在向量
在向量![]() =(0,4,
=(0,4,![]() )上的投影的絕對值,
)上的投影的絕對值,
由![]() ,得d=
,得d=![]() =
=![]()
所以點B到平面OCD的距離為![]() .
.


 黃岡創(chuàng)優(yōu)卷系列答案
黃岡創(chuàng)優(yōu)卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知以![]() 為首項的數(shù)列
為首項的數(shù)列![]() 滿足:
滿足: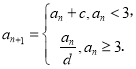
(1)當(dāng)![]() ,
,![]() 時,求數(shù)列
時,求數(shù)列![]() 的通項公式;
的通項公式;
(2)當(dāng)![]() ,
,![]() 時,試用
時,試用![]() 表示數(shù)列
表示數(shù)列![]() 前100項的和
前100項的和![]() ;
;
(3)當(dāng)![]() (
(![]() 是正整數(shù)),
是正整數(shù)),![]() ,正整數(shù)
,正整數(shù)![]() 時,判斷數(shù)列
時,判斷數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() 是否成等比數(shù)列?并說明理由.
是否成等比數(shù)列?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)集![]() 由實數(shù)構(gòu)成,且滿足:若
由實數(shù)構(gòu)成,且滿足:若![]() (
(![]() 且
且![]() ),則
),則![]() .
.
(1)若![]() ,試證明
,試證明![]() 中還有另外兩個元素;
中還有另外兩個元素;
(2)集合![]() 是否為雙元素集合,并說明理由;
是否為雙元素集合,并說明理由;
(3)若![]() 中元素個數(shù)不超過8個,所有元素的和為
中元素個數(shù)不超過8個,所有元素的和為![]() ,且
,且![]() 中有一個元素的平方等于所有元素的積,求集合
中有一個元素的平方等于所有元素的積,求集合![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于任意的![]() ,若數(shù)列
,若數(shù)列![]() 同時滿足下列兩個條件,則稱數(shù)列
同時滿足下列兩個條件,則稱數(shù)列![]() 具有“性質(zhì)m”:
具有“性質(zhì)m”:![]() ;
;![]() 存在實數(shù)M,使得
存在實數(shù)M,使得![]() 成立.
成立.
![]() 數(shù)列
數(shù)列![]() 、
、![]() 中,
中,![]() 、
、![]() (
(![]() ),判斷
),判斷![]() 、
、![]() 是否具有“性質(zhì)m”;
是否具有“性質(zhì)m”;
![]() 若各項為正數(shù)的等比數(shù)列
若各項為正數(shù)的等比數(shù)列![]() 的前n項和為
的前n項和為![]() ,且
,且![]() ,
,![]() ,求證:數(shù)列
,求證:數(shù)列![]() 具有“性質(zhì)m”;
具有“性質(zhì)m”;
![]() 數(shù)列
數(shù)列![]() 的通項公式
的通項公式![]() 對于任意
對于任意![]() ,數(shù)列
,數(shù)列![]() 具有“性質(zhì)m”,且對滿足條件的M的最小值
具有“性質(zhì)m”,且對滿足條件的M的最小值![]() ,求整數(shù)t的值.
,求整數(shù)t的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在邊長為2的菱形![]() 中,
中,![]() ,將菱形
,將菱形![]() 沿對角線
沿對角線![]() 對折,使二面角
對折,使二面角![]() 的余弦值為
的余弦值為![]() ,則所得三棱錐
,則所得三棱錐![]() 的內(nèi)切球的表面積為( )
的內(nèi)切球的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校共有教職工900人,分成三個批次進(jìn)行繼續(xù)教育培訓(xùn),在三個批次中男、女教職工人數(shù)如下表所示.已知在全體教職工中隨機抽取一名,抽到第二批次中女職工的概率是0.16.
第一批次 | 第二批次 | 第三批次 | |
女教職工 | 196 |
|
|
男教職工 | 204 | 156 |
|
(1)求![]() 的值;
的值;
(2)現(xiàn)用分層抽樣的方法在全體教職工中抽取54名做培訓(xùn)效果的調(diào)查,問應(yīng)在第三批次中抽取教職工多少名?
(3)已知![]() ,
,![]() ,求第三批次中女教職工比男教職工多的概率.
,求第三批次中女教職工比男教職工多的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在三棱錐![]() 中,底面
中,底面![]() 是邊長為 2 的正三角形,頂點
是邊長為 2 的正三角形,頂點 ![]() 在底面
在底面![]() 上的射影為
上的射影為![]() 的中心,若
的中心,若![]() 為
為![]() 的中點,且直線
的中點,且直線![]() 與底面
與底面![]() 所成角的正切值為
所成角的正切值為![]() ,則三棱錐
,則三棱錐![]() 外接球的表面積為( )
外接球的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com