
【題目】設函數f(x)= ![]() x3﹣(1+a)x2+4ax+24a,其中常數a>1
x3﹣(1+a)x2+4ax+24a,其中常數a>1
(1)討論f(x)的單調性;
(2)若當x≥0時,f(x)>0恒成立,求a的取值范圍.
【答案】
(1)解:f′(x)=x2﹣2(1+a)x+4a=(x﹣2)(x﹣2a),
由已知a>1,∴2a>2,∴令f′(x)>0,解得x>2a或x<2,
令f′(x)<0,解得2<x<2a,
故當a>1時,f(x)在區間(﹣∞,2)和(2a,+∞)上是增函數,在區間(2,2a)上是減函數.
(2)解:由(1)知,當x≥0時,f(x)在x=2a或x=0處取得最小值.
![]() =
= ![]() ,f(0)=24a.
,f(0)=24a.
則 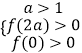 即
即  解得1<a<6,
解得1<a<6,
故a的取值范圍是(1,6).
【解析】(1)先求出導函數,利用導數大于0對應的為原函數的增區間,導數小于0對應的為原函數的減區間,即可求f(x)的單調性;(2)由(1)知,當x≥0時,f(x)在x=2a或x=0處取得最小值,所以須滿足最小值大于0,解不等式組 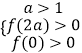 即可求a的取值范圍.
即可求a的取值范圍.
【考點精析】本題主要考查了利用導數研究函數的單調性和函數的最大(小)值與導數的相關知識點,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.
比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】近年來,“共享單車”的出現為市民“綠色出行”提供了極大的方便,某共享單車公司“Mobike”計劃在甲、乙兩座城市共投資120萬元,根據行業規定,每個城市至少要投資40萬元,由前期市場調研可知:甲城市收益P與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,乙城市收益Q與投入
,乙城市收益Q與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,設甲城市的投入為
,設甲城市的投入為![]() (單位:萬元),兩個城市的總收益為
(單位:萬元),兩個城市的總收益為![]() (單位:萬元).
(單位:萬元).
(1)當甲城市投資50萬元時,求此時公司總收益;
(2)試問如何安排甲、乙兩個城市的投資,才能使總收益最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的一段圖象如圖5所示:將
的一段圖象如圖5所示:將![]() 的圖像向右平移
的圖像向右平移![]() 個單位,可得到函數
個單位,可得到函數![]() 的圖象,且圖像關于原點對稱,
的圖象,且圖像關于原點對稱,

(1)求![]() 的值;
的值;
(2)求![]() 的最小值,并寫出
的最小值,并寫出![]() 的表達式;
的表達式;
(3)若關于![]() 的函數
的函數![]() 在區間
在區間![]() 上最小值為
上最小值為![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A. 線性回歸直線![]() 至少經過其樣本數據點中的一個點
至少經過其樣本數據點中的一個點
B. 在統計學中,獨立性檢驗是檢驗兩個分類變量是否有關系的一種統計方法
C. 在回歸分析中,相關指數![]() 越大,模擬的效果越好
越大,模擬的效果越好
D. 在殘差圖中,殘差分布的帶狀區域的寬度越狹窄,其模擬的效果越好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,直線
,直線![]() ,且點
,且點![]() 不在直線
不在直線![]() 上.
上.
(1)若點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,求
,求![]() 點坐標;
點坐標;
(2)求證:點![]() 到直線
到直線![]() 的距離
的距離![]() ;
;
(3)當點![]() 在函數
在函數![]() 圖像上時,(2)中的公式變為
圖像上時,(2)中的公式變為![]() ,
,
請參考該公式,求![]()
![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將邊長為1的正方形![]() 沿對角線
沿對角線![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,在折起后形成的三棱錐
,在折起后形成的三棱錐![]() 中,給出下列三種說法:
中,給出下列三種說法:
①![]() 是等邊三角形;②
是等邊三角形;②![]() ;③三棱錐
;③三棱錐![]() 的體積是
的體積是![]() .
.
其中正確的序號是__________(寫出所有正確說法的序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com