
【題目】如圖,四邊形ABCD是棱長為2的正方形,E為AD的中點,以CE為折痕把△DEC折起,使點D到達點P的位置,且點P的射影O落在線段AC上.
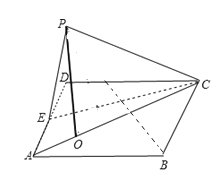
(1)求![]() ;
;
(2)求幾何體P﹣ABCE的體積.
 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:高中數學 來源: 題型:
【題目】如圖,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是線段EF上的動點
AC,P是線段EF上的動點
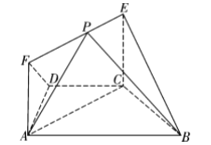
(1)求證:平面BCE⊥平面ACEF;
(2)求平面PAB與平面BCE所成銳二面角![]() 的最小值
的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,直線的方程為2ρcosθ+5ρsinθ﹣8=0,曲線E的方程為ρ=4cosθ.
(1)以極點O為直角坐標原點,極軸為x軸正半軸建立平面直角坐標系,分別寫出直線l與曲線E的直角坐標方程;
(2)設直線l與曲線E交于A,B兩點,點C在曲線E上,求△ABC面積的最大值,并求此時點C的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=loga(1+x)+loga(3﹣x)(a>0,a≠1)且f(1)=2.
(1)求a的值及f(x)的定義域;
(2)求f(x)在區間[0,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元前![]() 世紀的畢達哥拉斯是最早研究“完全數”的人.完全數是一種特殊的自然數,它所有的真因子(即除了自身以外的約數)的和恰好等于它本身.若從集合
世紀的畢達哥拉斯是最早研究“完全數”的人.完全數是一種特殊的自然數,它所有的真因子(即除了自身以外的約數)的和恰好等于它本身.若從集合![]() 中隨機抽取兩個數,則這兩個數中有完全數的概率是______.
中隨機抽取兩個數,則這兩個數中有完全數的概率是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
在直角坐標系xOy中,設傾斜角為α的直線l:![]() (t為參數)與曲線C:
(t為參數)與曲線C:![]() (θ為參數)相交于不同的兩點A,B.
(θ為參數)相交于不同的兩點A,B.
(Ⅰ)若α=![]() ,求線段AB中點M的坐標;
,求線段AB中點M的坐標;
(Ⅱ)若|PA|·|PB|=|OP|![]() ,其中P(2,
,其中P(2,![]() ),求直線l的斜率.
),求直線l的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com