【題目】下列命題：
①“四邊相等的四邊形是正方形”的否命題；
②“梯形不是平行四邊形”的逆否命題；
③“若 
，則 
”的逆命題.
其中真命題是.
【答案】①②
【解析】①“四邊相等的四邊形是正方形”的否命題為“正方形的四條邊相等”，該命題為真命題，
②命題“梯形不是平行四邊形”是真命題，則其逆否命題是真命題；
“若 
，則 
”的逆命題是“若 ，則 ”
③當 
時，該命題為假命題.
綜上可得，真命題是①②.
【考點精析】根據題目的已知條件，利用四種命題的真假關系和命題的真假判斷與應用的相關知識可以得到問題的答案，需要掌握一個命題的真假與其他三個命題的真假有如下三條關系：(原命題 逆否命題)①、原命題為真，它的逆命題不一定為真;②、原命題為真，它的否命題不一定為真;③、原命題為真，它的逆否命題一定為真；兩個命題互為逆否命題，它們有相同的真假性；兩個命題為互逆命題或互否命題，它們的真假性沒有關系．
名校通行證有效作業系列答案科目：高中數學 來源： 題型：
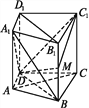
【題目】如圖,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,點M是棱BB1上一點.
(1)求證:B1D1∥平面A1BD;
(2)求證:MD⊥AC;
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義域為
的函數
滿足：
，且對于任意實數
，
恒有
，當
時，
.
（1）求
的值，并證明當
時，
；
（2）判斷函數在上的單調性并加以證明；
（3）若不等式
對任意
恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）
如圖，在四棱錐P—ABCD中，側面PAD⊥底面ABCD，側棱PA＝PD=
,底面ABCD為直角梯形，其中BC∥AD,AB⊥AD,AD=2AB=2BC=2，O為AD中點.
(Ⅰ)求證:PO⊥平面ABCD；
(Ⅱ)求異面直線PB與CD所成角的余弦值；
(Ⅲ)求點A到平面PCD的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(本題滿分14分)
已知正項數列
滿足：對任意正整數
，都有
成等差數列，
成等比數列，且
（Ⅰ）求證：數列
是等差數列；
（Ⅱ）求數列的通項公式；
(Ⅲ) 設
如果對任意正整數，不等式
恒成立，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓 
經過點 
,離心率為 
,左、右焦點分別為 
．
（1）求橢圓的方程;
（2）若直線 
與橢圓交于A,B兩點,與以 
為直徑的圓交于C,D兩點,求 
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓 
，圓心為 
，定點 
， 
為圓 上一點，線段 
上一點 
滿足 
，直線 
上一點 
，滿足 
．
（Ⅰ）求點 的軌跡 
的方程；
（Ⅱ） 
為坐標原點， 
是以 
為直徑的圓，直線 
與 相切，并與軌跡 交于不同的兩點 
．當 
且滿足 
時，求 
面積 
的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
