
【題目】定義域?yàn)?/span>![]() 的函數(shù)
的函數(shù)![]() 滿足:
滿足:![]() ,且對(duì)于任意實(shí)數(shù)
,且對(duì)于任意實(shí)數(shù)![]() ,
,![]() 恒有
恒有![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() .
.
(1)求![]() 的值,并證明當(dāng)
的值,并證明當(dāng)![]() 時(shí),
時(shí),![]() ;
;
(2)判斷函數(shù)![]() 在
在![]() 上的單調(diào)性并加以證明;
上的單調(diào)性并加以證明;
(3)若不等式![]() 對(duì)任意
對(duì)任意![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)見解析;(3)![]() 或
或![]()
【解析】分析:(1)賦值:令![]() ,
,![]() ,可得
,可得![]() ,令
,令![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,
,![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,
,![]() ,所以
,所以![]() .(2)單調(diào)性證明根據(jù)定義證明即可:設(shè)
.(2)單調(diào)性證明根據(jù)定義證明即可:設(shè)![]() ,則
,則![]() ,
,![]() ,
,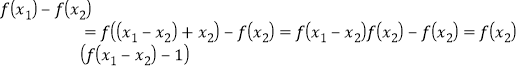 ,由(1)知
,由(1)知![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,(3)結(jié)合(2)的單調(diào)性可得只需解
,(3)結(jié)合(2)的單調(diào)性可得只需解![]() ,對(duì)任意
,對(duì)任意![]() 恒成立即可.
恒成立即可.
詳解:
(1)由已知,對(duì)于任意實(shí)數(shù)![]() ,
,![]() 恒有
恒有![]() ,
,
令![]() ,
,![]() ,可得
,可得![]() ,
,
因?yàn)楫?dāng)![]() 時(shí),
時(shí),![]() ,所以
,所以![]() ,故
,故![]() .
.
令![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,
,![]() ,
,
因?yàn)?/span>![]() ,
,![]() ,所以
,所以![]() .
.
(2)設(shè)![]() ,則
,則![]() ,
,![]() ,
,
![]()
![]() ,
,
由(1)知![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以函數(shù)![]() 在
在![]() 上為減函數(shù).
上為減函數(shù).
(3)由![]() 得
得![]()
所以![]()
即![]() ,
,
上式等價(jià)于![]() 對(duì)任意
對(duì)任意![]() 恒成立,
恒成立,
因?yàn)?/span>![]() ,所以
,所以![]()
所以![]() 對(duì)任意
對(duì)任意![]() 恒成立,
恒成立,
設(shè)![]() ,
,![]() (
(![]() 時(shí)取等),
時(shí)取等),
所以![]() ,
,
解得![]() 或
或![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線 ![]() 的頂點(diǎn)在原點(diǎn)
的頂點(diǎn)在原點(diǎn) ![]() ,對(duì)稱軸是
,對(duì)稱軸是 ![]() 軸,且過點(diǎn)
軸,且過點(diǎn) ![]() .
.
(Ⅰ)求拋物線 ![]() 的方程;
的方程;
(Ⅱ)已知斜率為 ![]() 的直線
的直線 ![]() 交
交 ![]() 軸于點(diǎn)
軸于點(diǎn) ![]() ,且與曲線
,且與曲線 ![]() 相切于點(diǎn)
相切于點(diǎn) ![]() ,點(diǎn)
,點(diǎn) ![]() 在曲線
在曲線 ![]() 上,且直線
上,且直線 ![]() 軸,
軸, ![]() 關(guān)于點(diǎn)
關(guān)于點(diǎn) ![]() 的對(duì)稱點(diǎn)為
的對(duì)稱點(diǎn)為 ![]() ,判斷點(diǎn)
,判斷點(diǎn) ![]() 是否共線,并說明理由.
是否共線,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題p:實(shí)數(shù)x滿足 ![]() ,其中
,其中 ![]() ;和命題q:實(shí)數(shù)x滿足
;和命題q:實(shí)數(shù)x滿足 ![]() .
.
(1)若a=1且p∧q為真,求實(shí)數(shù)x的取值范圍;
(2)若-p是-q的充分不必要條件,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某廠家舉行大型的促銷活動(dòng),經(jīng)測算某產(chǎn)品當(dāng)促銷費(fèi)用為x萬元時(shí),銷售量t萬件滿足t=5- ![]() (其中0
(其中0 ![]() x
x ![]() a,a為正常數(shù)),現(xiàn)假定生產(chǎn)量與銷售量相等,已知生產(chǎn)該產(chǎn)品t萬件還需投入成本(10+2t)萬元(不含促銷費(fèi)用),產(chǎn)品的銷售價(jià)格定為5+
a,a為正常數(shù)),現(xiàn)假定生產(chǎn)量與銷售量相等,已知生產(chǎn)該產(chǎn)品t萬件還需投入成本(10+2t)萬元(不含促銷費(fèi)用),產(chǎn)品的銷售價(jià)格定為5+ ![]() 萬元/萬件.
萬元/萬件.
(1)將該產(chǎn)品的利潤y萬元表示為促銷費(fèi)用x萬元的函數(shù);
(2)促銷費(fèi)用投入多少萬元時(shí),廠家的利潤最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角坐標(biāo)系xoy中,其中A(0,0),B(2,0),C(1,1),D(0,1),圖中圓弧所在圓的圓心為點(diǎn)C,半徑為 ![]() ,且點(diǎn)P在圖中陰影部分(包括邊界)運(yùn)動(dòng).若
,且點(diǎn)P在圖中陰影部分(包括邊界)運(yùn)動(dòng).若 ![]() ,其中
,其中 ![]() ,則
,則 ![]() 的取值范圍是( )
的取值范圍是( )
A.[2,3+ ![]() ]
]
B.[2,3+ ![]() ]
]
C.[3- ![]() , 3+
, 3+ ![]() ]
]
D.[3- ![]() , 3+
, 3+ ![]() ]
]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]()
(1)若對(duì) ![]() ,f(x)
,f(x) ![]() 恒成立,求a的取值范圍;
恒成立,求a的取值范圍;
(2)已知常數(shù)a ![]() R,解關(guān)于x的不等式f(x)
R,解關(guān)于x的不等式f(x) ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題:
①“四邊相等的四邊形是正方形”的否命題;
②“梯形不是平行四邊形”的逆否命題;
③“若 ![]() ,則
,則 ![]() ”的逆命題.
”的逆命題.
其中真命題是.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的角A,B,C所對(duì)的邊分別為a,b,c,設(shè)向量![]() =(a,b),
=(a,b),![]() =(sin B,sin A),
=(sin B,sin A), ![]() =(b-2,a-2).
=(b-2,a-2).
(1)若![]() ∥
∥![]() ,求證:△ABC為等腰三角形;
,求證:△ABC為等腰三角形;
(2)若![]() ⊥
⊥![]() ,邊長c=2,∠C=
,邊長c=2,∠C=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com