Question

【題目】如圖，四棱錐P-ABCD中，底面為菱形，且， ．

（Ⅰ）求證： ；

（Ⅱ）若，求二面角的余弦值。

Answer 1

【答案】（1）證明見解析；（2）．

【解析】試題（1）取的中點，利用菱形和等邊三角形的三線合一得到線線垂直，進而得到線面垂直和線線垂直；（2）先利用勾股定理和線面垂直的判定定理得到線面垂直，建立空間直角坐標系，利用空間向量進行求解．

試題解析：（Ⅰ）證明：取的中點，連接．

∵，四邊形為菱形，且，

∴和為兩個全等的等邊三角形，

則

∴平面，又平面，

∴；

（Ⅱ）解：在中，由已知得， ， ，

則，∴，

即，又，∴平面；

以點E為坐標原點，分別以EA，EB，EP所在直線為x，y，z軸，建立如圖所示空間直角坐標系，

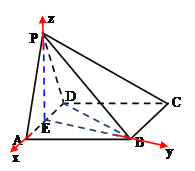
則E（0，0，0），C（－2， ，0），D（－1，0，0），P（0，0， ），

則＝（1，0， ），＝（－1， ，0），

由題意可設平面的一個法向量為；

設平面的一個法向量為，

由已知得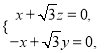： 令y＝1，則，z＝－1，

∴；

則，所以 ，

由題意知二面角的平面角為鈍角，

所以二面角的余弦值為