
分析 (1)a=0時,$f(x)=\left\{\begin{array}{l}{{x}^{2},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,分類討論滿足f(x)≥$\frac{1}{4}$的x值,可得答案;
(2)若f-1(4-a)≤f(x)在x∈[0,+∞)上恒成立,則f-1(4-a)≤a,進而得到實數a的取值范圍.
解答 解:(1)a=0時,$f(x)=\left\{\begin{array}{l}{{x}^{2},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,
∵$f(x)≥\frac{1}{4}$,
∴當x≥0時,f(x)=x2$≥\frac{1}{4}$,解得x≥$\frac{1}{2}$;
當x<0時,f(x)=${2}^{x}≥\frac{1}{4}$,解得-2≤x<0;
綜上,不等式$f(x)≥\frac{1}{4}$的解集為{x|-2≤x<0或x≥$\frac{1}{2}$};
(2)若函數y=f(x)存在反函數,
則函數f(x)在R為單調函數,則a≥1,
此時函數f(x)在R為單調遞增函數,
x∈[0,+∞)時,f(x)≥f(0)=a;
此時f-1(x)=$\left\{\begin{array}{l}\sqrt{x-a},x≥1\\{log}_{2}x,0<x<1\end{array}\right.$在(0,+∞)上也為增函數,
若關于x的不等式:f-1(4-a)≤f(x)在x∈[0,+∞)上恒成立,
則$\left\{\begin{array}{l}4-a>0\\{f}^{-1}(4-a)≤a\end{array}\right.$,
當0<4-a<1,即3<a<4時,log2(4-a)≤a恒成立,
當4-a≥1,即1≤a≤3時,解:$\sqrt{4-2a}≤a$得:-1+$\sqrt{5}$≤a≤2
綜上可得:a∈[-1+$\sqrt{5}$,2]∪(3,4).
點評 本題考查的知識點是分段函數的應用,反函數,函數恒成為問題,轉化思想,分類討論思想,難度中檔.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $(0,\frac{1}{2})∪(2,+∞)$ | B. | $(\frac{1}{2},1)∪(2,+∞)$ | C. | (2,+∞) | D. | $(\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
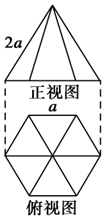 如圖是一個幾何體的正視圖和俯視圖.
如圖是一個幾何體的正視圖和俯視圖.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com