
【題目】設a為實數,函數f(x)=![]() +a
+a![]() +a
+a![]() .
.
(1)設t=![]() ,求t的取值范圖;
,求t的取值范圖;
(2)把f(x)表示為t的函數h(t);
(3)設f (x)的最大值為M(a),最小值為m(a),記g(a)=M(a)-m(a)求g(a)的表達式.
【答案】(1)[![]() ,2]; (2)h(t)=at+
,2]; (2)h(t)=at+![]() ,
,![]() ≤t≤2; (3)g(a)=
≤t≤2; (3)g(a)=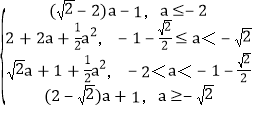 ..
..
【解析】
(1)將t=![]() 兩邊平方,結合二次函數的性質可得t的范圍;(2)由(1)可得
兩邊平方,結合二次函數的性質可得t的范圍;(2)由(1)可得![]() =
=![]() ,可得h(t)的解析式;(3)求得h(t)=
,可得h(t)的解析式;(3)求得h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,對稱軸為t=-a,討論對稱軸與區間[
a2,對稱軸為t=-a,討論對稱軸與區間[![]() ,2]的關系,結合單調性可得h(t)的最值,即可得到所求g(a)的解析式.
,2]的關系,結合單調性可得h(t)的最值,即可得到所求g(a)的解析式.
(1)t=![]() ,可得t2=2+2
,可得t2=2+2![]() ,
,
由0≤1-x2≤1,可得2≤t2≤4,
又t≥0可得![]() ≤t≤2,
≤t≤2,
即t的取值范圍是[![]() ,2];
,2];
(2)由(1)可得![]() =
=![]() ,
,
即有h(t)=at+![]() ,
,![]() ≤t≤2;
≤t≤2;
(3)由h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,
a2,
對稱軸為t=-a,
當-a≥2即a≤-2時,h(t)在[![]() ,2]遞減,
,2]遞減,
可得最大值M(a)=h(![]() )=
)=![]() a;最小值m(a)=h(2)=1+2a,
a;最小值m(a)=h(2)=1+2a,
則g(a)=(![]() -2)a-1;
-2)a-1;
當-a≤![]() 即a≥-
即a≥-![]() 時,h(t)在[
時,h(t)在[![]() ,2]遞增,
,2]遞增,
可得最大值M(a)=h(2)=1+2a;最小值m(a)=h(![]() )=
)=![]() a,
a,
則g(a)=(2-![]() )a+1;
)a+1;
當![]() <-a<2即-2<a<-
<-a<2即-2<a<-![]() 時,h(t)的最小值為m(a)=h(-a)=-1-
時,h(t)的最小值為m(a)=h(-a)=-1-![]() a2,
a2,
若-1-![]() ≤a<-
≤a<-![]() ,則h(2)≥h(
,則h(2)≥h(![]() ),可得h(t)的最大值為M(a)=h(2)=1+2a,
),可得h(t)的最大值為M(a)=h(2)=1+2a,
可得g(a)=2+2a+![]() a2;
a2;
若-2<a<-1-![]() ,則h(2)<h(
,則h(2)<h(![]() ),可得h(t)的最大值為M(a)=h(
),可得h(t)的最大值為M(a)=h(![]() )=
)=![]() a,
a,
可得g(a)=![]() a+1+
a+1+![]() a2;
a2;
綜上可得g(a)=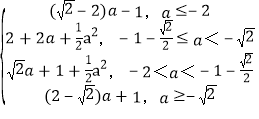 .
.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:高中數學 來源: 題型:
【題目】從甲、乙兩名學生中選拔一人參加射箭比賽,為此需要對他們的射箭水平進行測試.現這兩名學生在相同條件下各射箭10次,命中的環數如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)計算甲、乙兩人射箭命中環數的平均數和標準差;
(2)比較兩個人的成績,然后決定選擇哪名學生參加射箭比賽.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線C:x2=2py(p>0)的焦點為F,準線為l,A為C上一點,已知以F為圓心,FA為半徑的圓F交l于B,D兩點.
(1)若p=2且∠BFD=90°時,求圓F的方程;
(2)若A,B,F三點在同一直線m上,設直線m與拋物線C的另一個交點為E,在y軸上求一點G,使得∠OGE=∠OGA.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]()

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱錐P-ABCD的體積為
,且四棱錐P-ABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點的橢圓與雙曲線有公共焦點,且左、右焦點分別為F1、F2 , 這兩條曲線在第一象限的交點為P,△PF1F2 是以PF1為底邊的等腰三角形.若|PF1|=10,橢圓與雙曲線的離心率分別為e1、e2 , 則e1e2 的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 的值域為[0,+∞),求實數a的取值范圍;
的值域為[0,+∞),求實數a的取值范圍;
(2)若關于x的不等式F(x)>af(x)+12恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,根據長期收益率市場預測,投資![]() 類產品的收益與投資額成正比,投資
類產品的收益與投資額成正比,投資![]() 類產品的收益與投資額的算術平方根成正比.已知投資1萬元時
類產品的收益與投資額的算術平方根成正比.已知投資1萬元時![]() 兩類產品的收益分別為0.125萬元和0.5萬元.
兩類產品的收益分別為0.125萬元和0.5萬元.
(1)分別寫出![]() 兩類產品的收益與投資額的函數關系;
兩類產品的收益與投資額的函數關系;
(2)該家庭有20萬元資金,全部用于理財投資,問:怎么分配資金能使投資獲得最大收益,其最大收益是多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com