
【題目】已知函數![]() ,函數圖象在
,函數圖象在![]() 處的切線與x軸平行.
處的切線與x軸平行.
(1)討論方程![]() 根的個數;
根的個數;
(2)設![]() ,若對于任意的
,若對于任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]()
【解析】
(1)先根據函數圖象在![]() 處的切線與x軸平行可求
處的切線與x軸平行可求![]() 的值,然后求出函數的極值,從而可得根的個數;
的值,然后求出函數的極值,從而可得根的個數;
(2) 對于任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,可以轉化為
成立,可以轉化為![]() ,進而分別求解最值即可.
,進而分別求解最值即可.
解:(1)![]() ,
,
由題意知,![]() ,即
,即![]() ,解得
,解得![]() ,
,
故![]() ,此時
,此時![]() ,
,
則有:
x |
|
|
|
|
|
| + | 0 | - | td style="width:73.95pt; border-style:solid; border-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">+ | |
| 單調遞增 | 極大值 | 單調遞減 | 極小值 | 單調遞增 |
且當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() .
.
所以,當![]() 時,方程無根,當
時,方程無根,當![]() 或
或![]() 時,方程有一根,
時,方程有一根,
當![]() 或
或![]() 時,方程有兩個根,當
時,方程有兩個根,當![]() 時,方程有三個根;
時,方程有三個根;
(2)由題意可知,只需![]() ,
,
由(1)知,當![]() 時,
時,![]() ,
,
而![]() ,當
,當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞減,
單調遞減,![]() ,
,
所以![]() ,因為
,因為![]() ,無解,
,無解,
![]() ,
,![]() ,無解,
,無解,
![]() ,
,![]() ,
,![]() 在
在![]() 單調遞增,
單調遞增,![]() ,
,
此時,![]() ,
,
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】將余弦函數的圖象向右平移![]() 個單位后,再保持圖象上點的縱坐標不變,橫坐標變為原來的一半,得到函數
個單位后,再保持圖象上點的縱坐標不變,橫坐標變為原來的一半,得到函數![]() 的圖象,下列關于
的圖象,下列關于![]() 的敘述正確的是( )
的敘述正確的是( )
A. 最大值為![]() ,且關于
,且關于![]() 對稱
對稱
B. 周期為![]() ,關于直線
,關于直線![]() 對稱
對稱
C. 在![]() 上單調遞增,且為奇函數
上單調遞增,且為奇函數
D. 在![]() 上單調遞減,且為偶函數
上單調遞減,且為偶函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 為實數)有極值,且在
為實數)有極值,且在![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
(1)求實數![]() 的取值范圍;
的取值范圍;
(2)是否存在實數![]() ,使得函數
,使得函數![]() 的極小值為1,若存在,求出實數
的極小值為1,若存在,求出實數![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)設函數![]() 試證明:
試證明:![]() 在
在![]() 上恒成立并證明
上恒成立并證明![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠家具車間造![]() 、
、![]() 型兩類桌子,每張桌子需木工和漆工梁道工序完成.已知木工做一張
型兩類桌子,每張桌子需木工和漆工梁道工序完成.已知木工做一張![]() 、
、![]() 型型桌子分別需要1小時和2小時,漆工油漆一張
型型桌子分別需要1小時和2小時,漆工油漆一張![]() 、
、![]() 型型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張
型型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張![]() 、
、![]() 型型桌子分別獲利潤2千元和3千元.
型型桌子分別獲利潤2千元和3千元.
(1)列出滿足生產條件的數學關系式,并畫出可行域;
(2)怎樣分配生產任務才能使每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個多面體的直觀圖和三視圖如圖所示,點M是AB上的動點,記四面體EFMC的體積為V1,多面體ADF-BCE的體積為V2,則![]() =
=
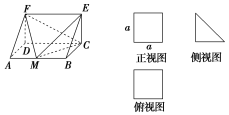
A.![]() B.
B.![]() C.
C.![]() D.不是定值,隨點M位置的變化而變化
D.不是定值,隨點M位置的變化而變化
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,地圖上有一豎直放置的圓形標志物,圓心為C,與地面的接觸點為G.與圓形標志物在同一平面內的地面上點P處有一個觀測點,且PG=50m.在觀測點正前方10m處(即PD=10m)有一個高位10m(即ED=10m)的廣告牌遮住了視線,因此在觀測點所能看到的圓形標志的最大部分即為圖中從A到F的圓弧.

(1)若圓形標志物半徑為25m,以PG所在直線為X軸,G為坐標原點,建立直角坐標系,求圓C和直線PF的方程;
(2)若在點P處觀測該圓形標志的最大視角(即![]() )的正切值為
)的正切值為![]() ,求該圓形標志物的半徑.
,求該圓形標志物的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com