
【題目】已知函數(shù)![]() ,
,![]() ,且
,且![]() 與
與![]() 的圖象有一條斜率為1的公切線(e為自然對數(shù)的底數(shù)).
的圖象有一條斜率為1的公切線(e為自然對數(shù)的底數(shù)).
(1)求![]() ;
;
(2)設(shè)函數(shù)![]() ,證明:當(dāng)
,證明:當(dāng)![]() 時,
時,![]() 有且僅有2個零點.
有且僅有2個零點.
【答案】(1)![]() ;(2)證明見解析
;(2)證明見解析
【解析】
(1)根據(jù)導(dǎo)數(shù)的幾何意義,分別求出函數(shù)![]() 圖象上斜率為1的切線,再根據(jù)切線方程為同一方程即可求出;
圖象上斜率為1的切線,再根據(jù)切線方程為同一方程即可求出;
(2)根據(jù)第一問結(jié)果可得,![]() ,求導(dǎo),換元,令
,求導(dǎo),換元,令![]() ,通過二次函數(shù)知識判斷
,通過二次函數(shù)知識判斷![]() 的符號,得其單調(diào)性,求出極值,再結(jié)合零點存在性定理即可求出.
的符號,得其單調(diào)性,求出極值,再結(jié)合零點存在性定理即可求出.
(1)令![]() ,可得
,可得![]() ,
,![]() .
.
![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,即
,即![]() .
.
令![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,即
,即![]() ,
,
故![]() ,
,
可得![]() .
.
(2)證明:由(1)可得![]() ,
,
![]() ,
,
令![]() ,則
,則![]() ,
,![]() ,
,
當(dāng)![]() 時,
時,![]() 有兩根
有兩根![]() ,
,![]() 且
且![]() ,
,
由![]() ,得
,得![]() ,
,
在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,
,
此時,![]() .
.
又![]() 時,
時,![]() ,
,![]() 時,
時,![]() .
.
故在![]() 和
和![]() 上,
上,![]() 各有1個零點.
各有1個零點.
所以![]() 時,
時,![]() 有2個零點.
有2個零點.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,GH是東西方向的公路北側(cè)的邊緣線,某公司準(zhǔn)備在GH上的一點B的正北方向的A處建設(shè)一倉庫,設(shè)![]() ,并在公路北側(cè)建造邊長為
,并在公路北側(cè)建造邊長為![]() 的正方形無頂中轉(zhuǎn)站CDEF(其中EF在GH上),現(xiàn)從倉庫A向GH和中轉(zhuǎn)站分別修兩條道路AB,AC,已知AB=AC+1,且
的正方形無頂中轉(zhuǎn)站CDEF(其中EF在GH上),現(xiàn)從倉庫A向GH和中轉(zhuǎn)站分別修兩條道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式,并求出定義域;
的函數(shù)解析式,并求出定義域;
(2)如果中轉(zhuǎn)站四堵圍墻造價為10萬元/km,兩條道路造價為30萬元/km,問:![]() 取何值時,該公司建設(shè)中轉(zhuǎn)站圍墻和兩條道路總造價M最低.
取何值時,該公司建設(shè)中轉(zhuǎn)站圍墻和兩條道路總造價M最低.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側(cè)面BB1C1C為菱形,![]() .
.
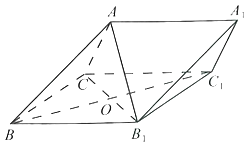
(1)求證:B1C⊥AB;
(2)若∠CBB1=60°,AC=BC,且點A在側(cè)面BB1C1C上的投影為點O,求二面角B﹣AA1﹣C的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體![]() 中,P,Q,M,N,H,R是各條棱的中點.
中,P,Q,M,N,H,R是各條棱的中點.
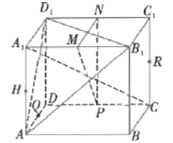
①直線![]() 平面
平面![]() ;②
;②![]() ;③P,Q,H,R四點共面;④
;③P,Q,H,R四點共面;④![]() 平面
平面![]() .其中正確的個數(shù)為( )
.其中正確的個數(shù)為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,直棱柱![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,點F,Q是棱
,點F,Q是棱![]() ,
,![]() 的中點,
的中點,![]() ,
,![]() 是棱
是棱![]() ,
,![]() 上的點,且
上的點,且![]() .
.
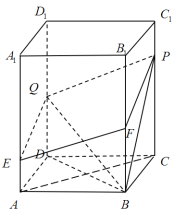
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)設(shè)曲線![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,求曲線在該點處的切線方程;
,求曲線在該點處的切線方程;
(Ⅱ)設(shè)方程![]() 有兩個實數(shù)根
有兩個實數(shù)根![]() ,
,![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】今年,新型冠狀病毒來勢兇猛,老百姓一時間“談毒色變”,近來,有關(guān)喝白酒可以預(yù)防病毒的說法一直在民間流傳,更有人拿出“醫(yī)”字的繁體字“醫(yī)”進行解讀為:醫(yī)治瘟疫要喝酒,為了調(diào)查喝白酒是否有助于預(yù)防病毒,我們調(diào)查了1000人的喝酒生活習(xí)慣與最終是否得病進行了統(tǒng)計,表格如下:
每周喝酒量(兩) |
|
|
|
|
|
人數(shù) | 100 | 300 | 450 | 100 |
|
規(guī)定:①每周喝酒量達到4兩的叫常喝酒人,反之叫不常喝酒人;
②每周喝酒量達到8兩的叫有酒癮的人.
(1)求![]() 值,從每周喝酒量達到6兩的人中按照分層抽樣選出6人,再從這6人中選出2人,求這2人中無有酒癮的人的概率;
值,從每周喝酒量達到6兩的人中按照分層抽樣選出6人,再從這6人中選出2人,求這2人中無有酒癮的人的概率;
(2)請通過上述表格中的統(tǒng)計數(shù)據(jù),填寫完下面的![]() 列聯(lián)表,并通過計算判斷是否能在犯錯誤的概率不超過0.1的前提下認為是否得病與是否常喝酒有關(guān)?并對民間流傳的說法做出你的判斷.
列聯(lián)表,并通過計算判斷是否能在犯錯誤的概率不超過0.1的前提下認為是否得病與是否常喝酒有關(guān)?并對民間流傳的說法做出你的判斷.
常喝酒 | 不常喝酒 | 合計 | |
得病 | |||
不得病 | 250 | 650 | |
合計 |
參考公式: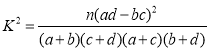 ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() 和
和![]() 都是定義在
都是定義在![]() 上的單調(diào)減函數(shù),且
上的單調(diào)減函數(shù),且![]() ,若對于任意
,若對于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 是
是![]() 在
在![]() 上的“被追逐函數(shù)”,若
上的“被追逐函數(shù)”,若![]() ,下述四個結(jié)論中正確的是( )
,下述四個結(jié)論中正確的是( )
①![]() 是
是![]() 在
在![]() 上的“被追逐函數(shù)”;
上的“被追逐函數(shù)”;
②若![]() 和函數(shù)
和函數(shù)![]() 關(guān)于
關(guān)于![]() 軸對稱,則
軸對稱,則![]() 是
是![]() 在
在![]() 上的“被追逐函數(shù)”;
上的“被追逐函數(shù)”;
③若![]() 是
是![]() 在
在![]() 上的“被追逐函數(shù)”,則
上的“被追逐函數(shù)”,則![]() ;
;
④存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函數(shù)”.
上的“被追逐函數(shù)”.
A.①③④B.①②④C.②③D.①③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
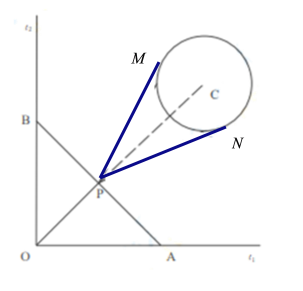
【題目】如圖,在一旅游區(qū)內(nèi)原有兩條互相垂直且相交于點O的道路l1,l2,一自然景觀的邊界近似為圓形,其半徑約為1千米,景觀的中心C到l1,l2的距離相等,點C到點O的距離約為10千米.現(xiàn)擬新建四條游覽道路方便游客參觀,具體方案:在線段OC上取一點P,新建一條道路OP,并過點P新建兩條與圓C相切的道路PM,PN(M,N為切點),同時過點P新建一條與OP垂直的道路AB(A,B分別在l1,l2上).為促進沿途旅游經(jīng)濟,新建道路長度之和越大越好,求新建道路長度之和的最大值.(所有道路寬度忽略不計)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com