
【題目】函數![]() 和
和![]() 都是定義在
都是定義在![]() 上的單調減函數,且
上的單調減函數,且![]() ,若對于任意
,若對于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 是
是![]() 在
在![]() 上的“被追逐函數”,若
上的“被追逐函數”,若![]() ,下述四個結論中正確的是( )
,下述四個結論中正確的是( )
①![]() 是
是![]() 在
在![]() 上的“被追逐函數”;
上的“被追逐函數”;
②若![]() 和函數
和函數![]() 關于
關于![]() 軸對稱,則
軸對稱,則![]() 是
是![]() 在
在![]() 上的“被追逐函數”;
上的“被追逐函數”;
③若![]() 是
是![]() 在
在![]() 上的“被追逐函數”,則
上的“被追逐函數”,則![]() ;
;
④存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函數”.
上的“被追逐函數”.
A.①③④B.①②④C.②③D.①③
【答案】D
【解析】
先判斷![]() 與
與![]() 是否單調遞減,并求得最小值,再根據若
是否單調遞減,并求得最小值,再根據若![]() 是
是![]() 在
在![]() 上的“被追逐函數”,
上的“被追逐函數”,![]() ,則
,則![]() 可用
可用![]() 表示,利用
表示,利用![]() ,代入判斷其是否恒成立,即可判斷是否滿足“被追逐函數”,由此依次判斷①②③④
,代入判斷其是否恒成立,即可判斷是否滿足“被追逐函數”,由此依次判斷①②③④
對于①,![]() 和
和![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,
,
若![]() 是
是![]() 在
在![]() 上的“被追逐函數”,則對于任意
上的“被追逐函數”,則對于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即![]() ,所以
,所以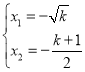 ,
,
此時![]() ,即
,即![]() ,構造函數
,構造函數![]() ,則
,則![]() ,則
,則![]() 在
在![]() 上單調遞減,又
上單調遞減,又![]() ,則
,則![]() 恒成立,即
恒成立,即![]() ,故對任意
,故對任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,故①正確;
成立,故①正確;
對于②,依題意![]() ,則
,則![]() 和
和![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“被追逐函數”,則對于任意
上的“被追逐函數”,則對于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即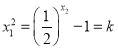 ,所以
,所以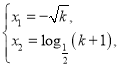 當
當![]() 時,不存在
時,不存在![]() ,
,![]() ,使得
,使得![]() 成立,故②錯誤;
成立,故②錯誤;
對于③,若![]() 是
是![]() 在
在![]() 上的“被追逐函數”,此時必有
上的“被追逐函數”,此時必有![]() ,解得
,解得![]() ,當
,當![]() 時,
時,![]() 和
和![]() 在
在![]() 上單調遞減,若
上單調遞減,若![]() 是
是![]() 在
在![]() 上的“被追逐函數”,則對于任意
上的“被追逐函數”,則對于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即![]() ,所以
,所以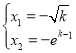 ,即
,即![]() ,則
,則![]() ,構造函數
,構造函數![]() ,則
,則![]() ,則
,則![]() 在
在![]() 上單調遞減,又
上單調遞減,又![]() ,則
,則![]() 恒成立,即
恒成立,即![]() ,故對任意
,故對任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,故③正確;
成立,故③正確;
對于④,當![]() 時,
時,![]() ,而當
,而當![]() 時,
時,![]() ,由
,由![]() 的任意性,不存在
的任意性,不存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函數”,故④錯誤,
上的“被追逐函數”,故④錯誤,
故選:D


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
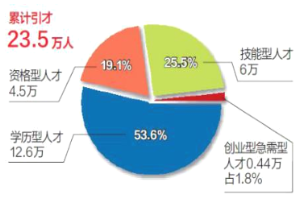
【題目】2020年1月1日《天津日報》發表文章總結天津海河英才計劃成果“厚植熱土 讓天下才天津用”——我市精細服務海河英才優化引才結構.“海河英才”行動計劃,緊緊圍繞“一基地三區”定位,聚焦戰略性新興產業人才需求,大力、大膽集聚人才.政策實施1年半以來,截至2019年11月30日,累計引進各類人才落戶23.5萬人.具體比例如圖所示,新引進兩院院士,長江學者,杰出青年科學基金獲得者等頂尖領軍人才112人.記者李軍計劃從人才庫中隨機選取一部分英才進行跟蹤調查采訪.
(1)李軍抽取了8人其中學歷型人才4人,技能型人才3人,資格型人才1人,周二和周五隨機進行采訪,每天4人(4人順序任意),周五采訪學歷型人才人數不超過2人的概率;
(2)李軍抽取不同類型的人才有不同的采訪補貼,學歷型人才500元/人,技能型人才400元/人,資格型人才600元/人,則創業型急需型人才最少補貼多少元/人使每名人才平均采訪補貼費用大于等于500元/人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三男生體育課上做投籃球游戲,兩人一組,每輪游戲中,每小組兩人每人投籃兩次,投籃投進的次數之和不少于![]() 次稱為“優秀小組”.小明與小亮同一小組,小明、小亮投籃投進的概率分別為
次稱為“優秀小組”.小明與小亮同一小組,小明、小亮投籃投進的概率分別為![]() .
.
(1)若![]() ,
,![]() ,則在第一輪游戲他們獲“優秀小組”的概率;
,則在第一輪游戲他們獲“優秀小組”的概率;
(2)若![]() 則游戲中小明小亮小組要想獲得“優秀小組”次數為
則游戲中小明小亮小組要想獲得“優秀小組”次數為![]() 次,則理論上至少要進行多少輪游戲才行?并求此時
次,則理論上至少要進行多少輪游戲才行?并求此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年底,武漢發生“新型冠狀病毒”肺炎疫情,國家衛健委緊急部署,從多省調派醫務工作者前去支援,正值農歷春節舉家團圓之際,他們成為“最美逆行者”.武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者疑似的新冠肺炎患者無法明確排除新冠肺炎的發熱患者和確診患者的密切接觸者等“四類”人員,強化網格化管理,不落一戶不漏一人.若在排查期間,某小區有5人被確認為“確診患者的密切接觸者”,現醫護人員要對這5人隨機進行逐一“核糖核酸”檢測,只要出現一例陽性,則將該小區確定為“感染高危小區”.假設每人被確診的概率均為![]() 且相互獨立,若當
且相互獨立,若當![]() 時,至少檢測了4人該小區被確定為“感染高危小區”的概率取得最大值,則
時,至少檢測了4人該小區被確定為“感染高危小區”的概率取得最大值,則![]() ____.
____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正四棱錐![]() 的側棱和底面邊長相等,在這個正四棱錐的
的側棱和底面邊長相等,在這個正四棱錐的![]() 條棱中任取兩條,按下列方式定義隨機變量
條棱中任取兩條,按下列方式定義隨機變量![]() 的值:
的值:
若這兩條棱所在的直線相交,則![]() 的值是這兩條棱所在直線的夾角大小(弧度制);
的值是這兩條棱所在直線的夾角大小(弧度制);
若這兩條棱所在的直線平行,則![]() ;
;
若這兩條棱所在的直線異面,則![]() 的值是這兩條棱所在直線所成角的大小(弧度制).
的值是這兩條棱所在直線所成角的大小(弧度制).
(1)求![]() 的值;
的值;
(2)求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的離心率
的離心率![]() ,左焦點為
,左焦點為![]() ,右頂點為
,右頂點為![]() ,過點
,過點![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點,若直線
兩點,若直線![]() 垂直于
垂直于![]() 軸時,有
軸時,有![]() .
.
(1)求橢圓的方程;
(2)設直線![]() :
: ![]() 上兩點
上兩點![]() ,
, ![]() 關于
關于![]() 軸對稱,直線
軸對稱,直線![]() 與橢圓相交于點
與橢圓相交于點![]() (
(![]() 異于點
異于點![]() ),直線
),直線![]() 與
與![]() 軸相交于點
軸相交于點![]() .若
.若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com