
分析 (1)根據題意,acosα+bsinα+c=0①,acosβ+bsinβ+c=0②;
①-②消去c,利用和差化積證出$\frac{a}{cos\frac{α+β}{2}}$=$\frac{b}{sin\frac{α+β}{2}}$;
①×cosβ-②cosα消去a,利用兩角差的正弦公式與和差化積證出$\frac{b}{sin\frac{α+β}{2}}$=$\frac{c}{cos\frac{α-β}{2}}$即可;
(2)由(1)平方,再利用合比公式即可求出cos2$\frac{α-β}{2}$的值.
解答 證明:(1)方程acosx+bsinx+c=0在(0,π)內有兩個相異的實根α、β,
∴acosα+bsinα+c=0,①
acosβ+bsinβ+c=0,②
∴方程①-②消去c得,
a(cosα-cosβ)+b(sinα-sinβ)=0,
即a(-2sin$\frac{α+β}{2}$sin$\frac{α-β}{2}$)+b(2cos$\frac{α+β}{2}$sin$\frac{α-β}{2}$)=0,
∴2sin$\frac{α-β}{2}$(bcos$\frac{α+β}{2}$-asin$\frac{α+β}{2}$)=0,
∵α≠β,∴sin$\frac{α-β}{2}$≠0,
∴bcos$\frac{α+β}{2}$-asin$\frac{α+β}{2}$=0,
∴$\frac{a}{cos\frac{α+β}{2}}$=$\frac{b}{sin\frac{α+β}{2}}$;
①×cosβ-②cosα消去a得:
bsinαcosβ-bsinβcosα+c(cosβ-cosα)=0,
∴bsin(α-β)=2csin$\frac{α+β}{2}$sin$\frac{α-β}{2}$,
即2bsin$\frac{α-β}{2}$cos$\frac{α-β}{2}$=2c•sin$\frac{α+β}{2}$sin$\frac{α-β}{2}$,
∴$\frac{b}{sin\frac{α+β}{2}}$=$\frac{c}{cos\frac{α-β}{2}}$;
即$\frac{a}{cos\frac{α+β}{2}}$=$\frac{b}{sin\frac{α+β}{2}}$=$\frac{c}{cos\frac{α-β}{2}}$;
(2)由(1)知,
$\frac{{c}^{2}}{{cos}^{2}\frac{α-β}{2}}$=$\frac{{a}^{2}}{{cos}^{2}\frac{α+β}{2}}$=$\frac{{b}^{2}}{{sin}^{2}\frac{α+β}{2}}$
=$\frac{{a}^{2}{+b}^{2}}{{cos}^{2}\frac{α+β}{2}{+sin}^{2}\frac{α+β}{2}}$
=a2+b2,
∴cos2$\frac{α-β}{2}$=$\frac{{c}^{2}}{{a}^{2}{+b}^{2}}$.
點評 本題考查了三角恒等變換的應用問題,也考查了三角恒等式的證明問題,是較難的題目.


科目:高中數學 來源: 題型:解答題
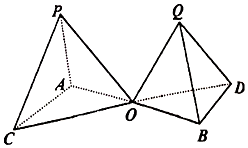 如圖所示的“相鄰塔”形立體建筑,已知P-OAC和Q-OBD是邊長分別為a和$\frac{m}{a}({m是常數})$的兩個正四面體,底面中AB與CD交于點O,試求出塔尖P,Q之間的距離關于邊長a的函數,并求出a為多少時,塔尖P,Q之間的距離最短.
如圖所示的“相鄰塔”形立體建筑,已知P-OAC和Q-OBD是邊長分別為a和$\frac{m}{a}({m是常數})$的兩個正四面體,底面中AB與CD交于點O,試求出塔尖P,Q之間的距離關于邊長a的函數,并求出a為多少時,塔尖P,Q之間的距離最短.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{{2}^{n}}$ | B. | n+$\frac{1}{{2}^{n}}$ | C. | n-$\frac{1}{{2}^{n}}$+1 | D. | n2-2n-$\frac{1}{{2}^{n}}$+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 概率為$\frac{1}{7}$ | B. | 頻率為$\frac{1}{7}$ | C. | 頻率為7 | D. | 概率接近$\frac{1}{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 9 | B. | $\frac{28}{3}$ | C. | $\frac{32}{3}$ | D. | 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({-∞\;,\;-\frac{2}{3}}]$ | B. | $[{\frac{2}{3}\;,\;+∞})$ | C. | $({-∞\;,\;-\frac{1}{2}}]$ | D. | $({-∞\;,\;\frac{1}{2}}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com