
【題目】請您設計一個帳篷.它下部的形狀是高為1m的正六棱柱,上部的形狀是側棱長為3m的正六棱錐(如圖所示).試問當帳篷的頂點O到底面中心O1的距離為多少時,帳篷的體積最大? 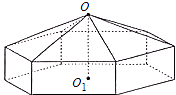
【答案】解:設OO1為xm,(1<x<4). 則由題設可得正六棱錐底面邊長為: ![]() (m).
(m).
(求解過程為: ![]() )
)
于是底面正六邊形的面積為(單位:m2) ![]()
帳篷的體積為(單位:m3) ![]() .
.
可得: ![]()
求導數,得 ![]()
令V'(x)=0解得x=﹣2(不合題意,舍去),x=2.
當1<x<2時,V'(x)>0,V(x)為增函數;
當2<x<4時,V'(x)<0,V(x)為減函數.
所以當x=2時,V(x)最大.
答當OO1為2m時,帳篷的體積最大.
【解析】設出頂點O到底面中心o1的距離,再求底面邊長和底面面積,求出體積表達式,利用導數求出高為何時體積取得最大值.
【考點精析】利用函數的最大(小)值與導數對題目進行判斷即可得到答案,需要熟知求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為R,f(1)=3,對任意x∈R,f′(x)<2,則f(x)<2x+1的解集為( )
A.(1,+∞)
B.(﹣1,1)
C.(﹣∞,1)
D.(﹣∞,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x)=x3﹣3x2 , 給出下列四個命題: ①f(x)是增函數,無極值;
②f(x)是減函數,有極值;
③f(x)在區間(﹣∞,0]及[2,+∞)上是增函數;
④f(x)有極大值為0,極小值﹣4;
其中正確命題的個數為( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區植被被破壞,土地沙化越來越嚴重,最近三年測得沙漠增加值分別為0.2萬公頃、0.4萬公頃、0.76萬公頃,則沙漠增加數y(萬公頃)關于年數x的函數關系較為近似的是( )
A.y=0.2x
B.![]()
C.![]()
D.y=0.2+log16x
查看答案和解析>>
科目:高中數學 來源: 題型:
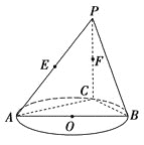
【題目】如圖,AB是圓O的直徑,點C是圓O上異于A,B的點,直線PC⊥平面ABC,E,F分別是PA,PC的中點.
(1)記平面BEF與平面ABC的交線為l,試判斷直線l與平面PAC的位置關系,并加以證明;
(2)設AB=PC=2,BC=1,求三棱錐P-BEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]()
(1)判斷f(x)的奇偶性并證明;
(2)若f(x)的定義域為[α,β](β>α>0),判斷f(x)在定義域上的增減性,并加以證明;
(3)若0<m<1,使f(x)的值域為[logmm(β﹣1),logmm(α﹣1)]的定義域區間[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com