Question

【題目】已知橢圓 =1（a＞b＞0）的一個頂點為A（0，1），離心率為 ，過點B（0，﹣2）及左焦點F1的直線交橢圓于C，D兩點，右焦點設為F2 ．
（1）求橢圓的方程；
（2）求△CDF2的面積．

Answer 1

【答案】
（1）解：∵橢圓 =1（a＞b＞0）的一個頂點為A（0，1），離心率為 ，

∴b= =1，且 = ，解之得a= ，c=1

可得橢圓的方程為

（2）解：∵左焦點F1（﹣1，0），B（0，﹣2），得F1B直線的斜率為﹣2

∴直線F1B的方程為y=﹣2x﹣2

由 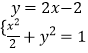，化簡得9x2+16x+6=0．

∵△=162﹣4×9×6=40＞0，

∴直線與橢圓有兩個公共點，設為C（x1，y1），D（x2，y2），

則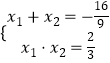

∴|CD|= |x1x2|= = =

又∵點F2到直線BF1的距離d= = ，

∴△CDF2的面積為S= |CD|×d= × =

【解析】（1）根據橢圓的基本概念和平方關系，建立關于a、b、c的方程，解出a= ，b=c=1，從而得到橢圓的方程；（2）求出F1B直線的斜率得直線F1B的方程為y=﹣2x﹣2，與橢圓方程聯解并結合根與系數的關系算出|xspan>1﹣x2|= ，結合弦長公式可得|CD|= ，最后利用點到直線的距離公式求出F2到直線BF1的距離d，即可得到△CDF2的面積．