
【題目】定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足
滿足![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ,函數(shù)
,函數(shù)![]() .若對(duì)任意
.若對(duì)任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立,則實(shí)數(shù)
成立,則實(shí)數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:先求出函數(shù)f(x)在![]() 的值域,再根據(jù)
的值域,再根據(jù)![]() ,求出函數(shù)f(x)在x
,求出函數(shù)f(x)在x![]() 時(shí)的值域和最小值,再利用導(dǎo)數(shù)求函數(shù)g(x)的最小值即得解.
時(shí)的值域和最小值,再利用導(dǎo)數(shù)求函數(shù)g(x)的最小值即得解.
詳解:由題得函數(shù)![]() 在[0,1]上的值域?yàn)?/span>
在[0,1]上的值域?yàn)?/span>![]() ,
,
函數(shù)![]()
![]() 在[1,
在[1,![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù),
上是增函數(shù),
所以函數(shù)在![]() 上的值域?yàn)?/span>
上的值域?yàn)?/span>![]() .
.
所以函數(shù)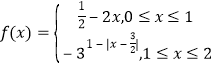 在
在![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ∪
∪![]() .
.
因?yàn)槎x在![]() 上的函數(shù)
上的函數(shù)![]() 滿足
滿足![]() ,
,
所以函數(shù)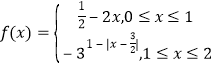 在
在![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ∪
∪![]() .
.
所以函數(shù)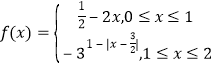 在
在![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ∪
∪![]() .
.
所以函數(shù)f(x)在![]() 的最小值為-12.
的最小值為-12.
∵函數(shù)g(x)=x3+3x2+m,
∴![]() =3x2+6x,
=3x2+6x,
令3x2+6x>0,所以x>0或x<﹣2,
令3x2+6x<0,所以﹣2<x<0,
∴函數(shù)g(x)=x3+3x2+m,在(﹣∞,﹣2),(0,+∞)單調(diào)遞增.在(﹣2,0)單調(diào)遞減,
∴t∈[﹣4,﹣2),g(t)最小=g(﹣4)=m﹣16,
∵不等式f(s)﹣g(t)≥0,
∴﹣12≥m﹣16,
故實(shí)數(shù)滿足m≤4,
故答案為:A


 七星圖書(shū)口算速算天天練系列答案
七星圖書(shū)口算速算天天練系列答案 初中學(xué)業(yè)考試導(dǎo)與練系列答案
初中學(xué)業(yè)考試導(dǎo)與練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中,將圓
中,將圓![]() 上每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉?lái)的
上每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉?lái)的![]() 倍,再把所得曲線上每一點(diǎn)向下平移1個(gè)單位得到曲線
倍,再把所得曲線上每一點(diǎn)向下平移1個(gè)單位得到曲線![]() .以
.以![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() .
.
(1)寫(xiě)出![]() 的參數(shù)方程和
的參數(shù)方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點(diǎn)![]() 在
在![]() 上,點(diǎn)
上,點(diǎn)![]() 在
在![]() 上,求使
上,求使![]() 取最小值時(shí)點(diǎn)
取最小值時(shí)點(diǎn)![]() 的直角坐標(biāo).
的直角坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為自然對(duì)數(shù)的底數(shù)).
為自然對(duì)數(shù)的底數(shù)).
(Ⅰ)若函數(shù)![]() 的圖象在
的圖象在![]() 處的切線為
處的切線為![]() ,當(dāng)實(shí)數(shù)
,當(dāng)實(shí)數(shù)![]() 變化時(shí),求證:直線
變化時(shí),求證:直線![]() 經(jīng)過(guò)定點(diǎn);
經(jīng)過(guò)定點(diǎn);
(Ⅱ)若函數(shù)![]() 有兩個(gè)極值點(diǎn),求實(shí)數(shù)
有兩個(gè)極值點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (
(![]() ),數(shù)列
),數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 圖象上,且
圖象上,且![]() 的最小值為
的最小值為![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)數(shù)列![]() 滿足
滿足 ,記數(shù)列
,記數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,“大衍數(shù)列”:![]() 來(lái)源于《乾坤譜》中對(duì)《易傳》“大衍之?dāng)?shù)五十”的推論,主要用于解釋中國(guó)傳統(tǒng)文化中的太極衍生過(guò)程中曾經(jīng)經(jīng)歷過(guò)的兩儀數(shù)量總和.下圖是求大衍數(shù)列前
來(lái)源于《乾坤譜》中對(duì)《易傳》“大衍之?dāng)?shù)五十”的推論,主要用于解釋中國(guó)傳統(tǒng)文化中的太極衍生過(guò)程中曾經(jīng)經(jīng)歷過(guò)的兩儀數(shù)量總和.下圖是求大衍數(shù)列前![]() 項(xiàng)和的程序框圖.執(zhí)行該程序框圖,輸入
項(xiàng)和的程序框圖.執(zhí)行該程序框圖,輸入![]() ,則輸出的
,則輸出的![]() ( )
( )


A. 64 B. 68 C. 100 D. 140
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),
時(shí),![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(3)若對(duì)任意的![]() ,
,![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】學(xué)校藝術(shù)節(jié)對(duì)同一類(lèi)的![]() 四項(xiàng)參賽作品,只評(píng)一項(xiàng)一等獎(jiǎng),在評(píng)獎(jiǎng)揭曉前,甲、乙、丙、丁四位同學(xué)對(duì)這四項(xiàng)參賽作品預(yù)測(cè)如下:
四項(xiàng)參賽作品,只評(píng)一項(xiàng)一等獎(jiǎng),在評(píng)獎(jiǎng)揭曉前,甲、乙、丙、丁四位同學(xué)對(duì)這四項(xiàng)參賽作品預(yù)測(cè)如下:
甲說(shuō):“![]() 或
或![]() 作品獲得一等獎(jiǎng)”;
作品獲得一等獎(jiǎng)”;
乙說(shuō):“![]() 作品獲得一等獎(jiǎng)”;
作品獲得一等獎(jiǎng)”;
丙說(shuō):“![]() ,
, ![]() 兩項(xiàng)作品未獲得一等獎(jiǎng)”;
兩項(xiàng)作品未獲得一等獎(jiǎng)”;
丁說(shuō):“![]() 作品獲得一等獎(jiǎng)”.
作品獲得一等獎(jiǎng)”.
若這四位同學(xué)只有兩位說(shuō)的話是對(duì)的,則獲得一等獎(jiǎng)的作品是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的中心在原點(diǎn),焦點(diǎn)在坐標(biāo)軸上,且經(jīng)過(guò)
的中心在原點(diǎn),焦點(diǎn)在坐標(biāo)軸上,且經(jīng)過(guò)![]() ,
,![]() .
.
(Ⅰ)求橢圓的標(biāo)準(zhǔn)方程和離心率;
(Ⅱ)四邊形![]() 的四個(gè)頂點(diǎn)都在橢圓
的四個(gè)頂點(diǎn)都在橢圓![]() 上,且對(duì)角線
上,且對(duì)角線![]() ,
,![]() 過(guò)原點(diǎn)
過(guò)原點(diǎn)![]() ,若
,若![]() ,求證:四邊形
,求證:四邊形![]() 的面積為定值,并求出此定值.
的面積為定值,并求出此定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).在以原點(diǎn)
為參數(shù)).在以原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正半軸為極軸的極坐標(biāo)系中,曲線
軸正半軸為極軸的極坐標(biāo)系中,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn),求
兩點(diǎn),求![]() .
.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com