
分析 根據f(x)、g(x)的圖象都經過點$P(0,\frac{1}{2})$,則sinθ=$\frac{1}{2}$,sin(-2φ+θ)=$\frac{1}{2}$,求得θ的值,可得-2φ+θ的值,從而求得φ的值.
解答 解:將函數$f(x)=sin(2x+θ)(|θ|<\frac{π}{2})$的圖象向右平移φ(0<φ<π)個單位長度后得到函數y=sin(2x-2φ+θ)的圖象,
∵f(x)、g(x)的圖象都經過點$P(0,\frac{1}{2})$,則sinθ=$\frac{1}{2}$,sin(-2φ+θ)=$\frac{1}{2}$,
∴θ=$\frac{π}{6}$,sin(-2φ+θ)=sin(-2φ+$\frac{π}{6}$)=$\frac{1}{2}$.
由于-2φ∈-2π,0),∴-2φ+$\frac{π}{6}$∈(-$\frac{11π}{6}$,$\frac{π}{6}$),∴-2φ+$\frac{π}{6}$=-$\frac{7π}{6}$,∴φ=$\frac{2π}{3}$.
故答案為:$\frac{2π}{3}$.
點評 本題考查的知識點是函數y=Asin(ωx+φ)的圖象變換,三角函數求值,屬于中檔題.


 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:解答題
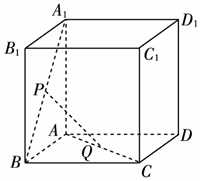 如圖所示,已知P、Q是單位正方體ABCD-A1B1C1D1的面A1B1BA和面ABCD對角線上的點,且A1P=AQ,證明:PQ∥平面BCC1B1.
如圖所示,已知P、Q是單位正方體ABCD-A1B1C1D1的面A1B1BA和面ABCD對角線上的點,且A1P=AQ,證明:PQ∥平面BCC1B1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $a=\sqrt{3}$,b=1 | |
| B. | 函數f(x)在區間$[{\frac{π}{6},π}]$上單調遞增 | |
| C. | 函數f(x)的圖象的一個對稱中心為$({\frac{2}{3}π,0})$ | |
| D. | 不等式f(x1)f(x2)≤4取到等號時|x2-x1|的最小值為2π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{3}{4}$ | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | 5 | C. | 15 | D. | 25 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 地區 | A | B | C |
| 數量 | 100 | 50 | 150 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com