
【題目】已知命題![]() 方程
方程![]() 在
在![]() 在存在唯一實數根;
在存在唯一實數根;![]() ,
,![]() .
.
(1)若命題![]() 為真命題,求實數
為真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() 為真命題,求實數
為真命題,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 為真命題得出
為真命題得出![]() ,可解出實數
,可解出實數![]() 的取值范圍;
的取值范圍;
(2)令![]() ,并作出函數
,并作出函數![]() 在區間
在區間![]() 上的圖象,得出當直線
上的圖象,得出當直線![]() 與函數
與函數![]() 在
在![]() 上只有一個交點時實數
上只有一個交點時實數![]() 的取值范圍,可得出命題
的取值范圍,可得出命題![]() 為真命題時實數
為真命題時實數![]() 的取值范圍,由命題
的取值范圍,由命題![]() 為真命題得出
為真命題得出![]() ,解出對應的實數
,解出對應的實數![]() 的取值范圍,再將
的取值范圍,再將![]() 的兩個取值范圍取交集可得出命題
的兩個取值范圍取交集可得出命題![]() 為真命題時
為真命題時![]() 的取值范圍.
的取值范圍.
(1)![]() ,
,![]() .
.
則命題![]() 為真命題時,有
為真命題時,有![]() ,則
,則![]() 或
或![]() .
.
因此,實數![]() 的取值范圍是
的取值范圍是![]() ;
;
(2)若命題![]() 為真命題,則
為真命題,則![]() 真且
真且![]() 真.
真.
命題![]() 為真命題時,即方程
為真命題時,即方程![]() 在
在![]() 上存在唯一實數根,
上存在唯一實數根,
令![]() ,則函數
,則函數![]() 在
在![]() 上單調遞增,
上單調遞增,
問題轉化為![]() ,在
,在![]() 上存在唯一實數根,
上存在唯一實數根,
令![]() ,則
,則![]() ,
,![]() .
.
作出函數![]() 在
在![]() 上的圖象如下圖所示:
上的圖象如下圖所示:
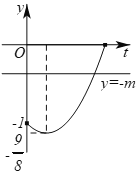
由圖象可知,當![]() 或
或![]() 時,即當
時,即當![]() 或
或![]() 時,直線
時,直線![]() 與函數
與函數![]() 在
在![]() 上有唯一交點.
上有唯一交點.
當命題![]() 為真命題時,有
為真命題時,有![]() ,則
,則![]() .
.
因此,當![]() 為真命題時,
為真命題時,![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知A是圓O:x2+y2=4上一動點,過點A作AB⊥x軸,垂足為B,動點D滿足![]() .
.
(1)求動點D的軌跡C的方程;
(2)垂直于x軸的直線M交軌跡C于M、N兩點,點P(3,0),直線PM與軌跡C的另一個交點為Q.問:直線NQ是否過一定點?若過定點,求出該定點的坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一片森林原來面積為![]() ,計劃每年砍伐一些樹,且每年砍伐面積的百分比相等,當砍伐到面積的一半時,所用時間是10年,為保護生態環境,森林面積至少要保留原面積的
,計劃每年砍伐一些樹,且每年砍伐面積的百分比相等,當砍伐到面積的一半時,所用時間是10年,為保護生態環境,森林面積至少要保留原面積的![]() ,已知到今年為止,森林剩余面積為原來的
,已知到今年為止,森林剩余面積為原來的![]() .
.
(1)到今年為止,該森林已砍伐了多少年?
(2)今后最多還能砍伐多少年?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點![]() 到定點
到定點![]() 的距離比
的距離比![]() 到定直線
到定直線![]() 的距離小
的距離小![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 任意作互相垂直的兩條直線
任意作互相垂直的兩條直線![]() ,
,![]() ,分別交曲線
,分別交曲線![]() 于點
于點![]() ,
,![]() 和
和![]() ,
,![]() .設線段
.設線段![]() ,
,![]() 的中點分別為
的中點分別為![]() ,
,![]() ,求證:直線
,求證:直線![]() 恒過一個定點;
恒過一個定點;
(3)在(2)的條件下,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
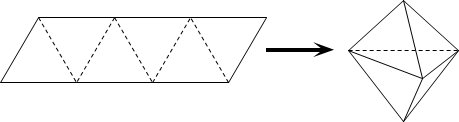
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽籺,俗稱“粽子”,古稱“角黍”,是端午節大家都會品嘗的食品,傳說這是為了紀念戰國時期楚國大臣、愛國主義詩人屈原.如圖,平行四邊形形狀的紙片是由六個邊長為1的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為____;若該六面體內有一球,則該球體積的最大值為____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校共有![]() 名學生,其中男生
名學生,其中男生![]() 人,為了解該校學生在學校的月消費情況,采取分層抽樣隨機抽取了
人,為了解該校學生在學校的月消費情況,采取分層抽樣隨機抽取了![]() 名學生進行調查,月消費金額分布在
名學生進行調查,月消費金額分布在![]() 之間.根據調查的結果繪制的學生在校月消費金額的頻率分布直方圖如圖所示:
之間.根據調查的結果繪制的學生在校月消費金額的頻率分布直方圖如圖所示:
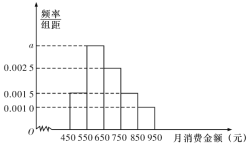
將月消費金額不低于![]() 元的學生稱為“高消費群”.
元的學生稱為“高消費群”.
(1)求![]() 的值,并估計該校學生月消費金額的平均數(同一組中的數據用該組區間的中點值作代表);
的值,并估計該校學生月消費金額的平均數(同一組中的數據用該組區間的中點值作代表);
(2)現采用分層抽樣的方式從月消費金額落在![]() ,
,![]() 內的兩組學生中抽取
內的兩組學生中抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人,記被抽取的
人,記被抽取的![]() 名學生中屬于“高消費群”的學生人數為隨機變量
名學生中屬于“高消費群”的學生人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望;
的分布列及數學期望;
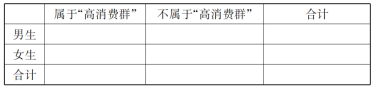
(3)若樣本中屬于“高消費群”的女生有![]() 人,完成下列
人,完成下列![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為該校學生屬于“高消費群”與“性別”有關?
的把握認為該校學生屬于“高消費群”與“性別”有關?
(參考公式: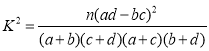 ,其中
,其中![]() )
)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且橢圓C過點
,且橢圓C過點![]() .
.
(1)求橢圓C的標準方程;
(2)過橢圓C的右焦點的直線l與橢圓C交于A、B兩點,且與圓:![]() 交于E、F兩點,求
交于E、F兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com