
已知函數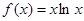 ,
,
(1)求函數 在
在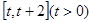 上的最小值;
上的最小值;
(2)若函數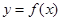 與
與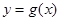 的圖像恰有一個公共點,求實數a的值;
的圖像恰有一個公共點,求實數a的值;
(3)若函數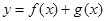 有兩個不同的極值點
有兩個不同的極值點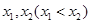 ,且
,且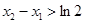 ,求實數a的取值范圍。
,求實數a的取值范圍。
(1)當 時最小值
時最小值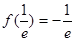 ,當
,當 時最小值
時最小值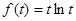 (2)3(3)
(2)3(3)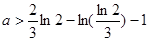
【解析】
試題分析:(1)令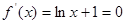 ,得
,得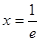 ,①當
,①當 時,函數
時,函數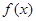 在
在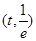 上單調遞減,在
上單調遞減,在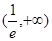 上單調遞增。此時最小值為
上單調遞增。此時最小值為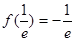 ;②當
;②當 時,函數在
時,函數在 上單調遞增,此時最小值為
上單調遞增,此時最小值為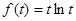 。
。
(2) 在
在 上有且僅有僅有一個根,即
上有且僅有僅有一個根,即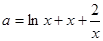 在
在 上有且僅有僅有一個根,令
上有且僅有僅有一個根,令 ,則
,則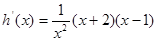 ,
,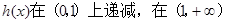 上遞增,所以
上遞增,所以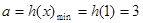 。
。
(3)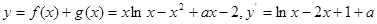 ,由題意知
,由題意知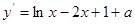 有兩個不同的實數根
有兩個不同的實數根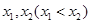 ,等價于
,等價于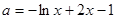 有兩個不同的實數根
有兩個不同的實數根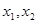 ,等價于直線
,等價于直線 與函數
與函數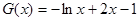 的圖像有兩個不同的交點。
的圖像有兩個不同的交點。
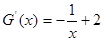 ,
, 所以當
所以當 時,
時,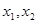 存在,且
存在,且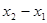 的值隨著
的值隨著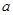 的增大而增大。
的增大而增大。
而當 時,則有
時,則有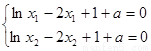 ,兩式相減得
,兩式相減得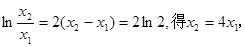 代入
代入 ,解得
,解得 此時
此時 ,所以實數
,所以實數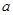 的取值范圍為
的取值范圍為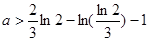
考點:函數單調性最值
點評:第一小題求最值需對參數分情況討論從而確定最值點的位置,第二小題將方程的根的情況轉化為函數最值得判定,這種轉化方法包括將不等式恒成立問題轉化為函數最值問題都是函數題目中經常用到的思路,須加以重視


 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:高中數學 來源:2011-2012學年人教版高一(上)期中數學試卷(解析版) 題型:解答題
 .
. 在(0,+∞)上是減函數.
在(0,+∞)上是減函數.查看答案和解析>>
科目:高中數學 來源:2010年上海市奉賢區高考數學二模試卷(文科)(解析版) 題型:解答題
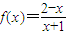 ;
; 成立,若存在求出x;若不存在,請說明理由.
成立,若存在求出x;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:2013屆浙江省高二下期中數學試卷(解析版) 題型:解答題
已知函數 令
令
(1)求 的定義域;
的定義域;
(2)判斷函數 的奇偶性,并予以證明;
的奇偶性,并予以證明;
(3)若 ,猜想
,猜想 之間的關系并證明.
之間的關系并證明.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市高三入學測試數學卷 題型:解答題
(本小題滿分12分)
已知函數 ,
,
(1)求函數 的定義域;(2)證明:
的定義域;(2)證明: 是偶函數;
是偶函數;
(3)若 ,求
,求 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com