
【題目】設函數![]() .
.
(1)若![]() ,
,![]() ,求函數
,求函數![]() 的極值;
的極值;
(2)若![]() 是函數
是函數![]() 的一個極值點,試求出
的一個極值點,試求出![]() 關于
關于![]() 的關系式(即用
的關系式(即用![]() 表示
表示![]() ),并確定
),并確定![]() 的單調區間;(提示:應注意對
的單調區間;(提示:應注意對![]() 的取值范圍進行討論)
的取值范圍進行討論)
(3)在(2)的條件下,設![]() ,函數
,函數![]() ,若存在
,若存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ,見解析; (3)
,見解析; (3)![]() .
.
【解析】
(1)求出導函數的根,判斷根左右兩邊導函數的符號,得到函數的單調性,據極大值極小值的定義求出極值;(2)據極值點處的導函數值為0得到a,b的關系;代入導函數中求出導函數的兩根,討論兩根的大小;判斷根左右兩邊導函數的符號,據導函數與單調性的關系求出單調區間;(3)據函數的單調性求出兩個函數的值域,求出函數值的最小距離,最小距離小于1求出a的范圍
(1)∵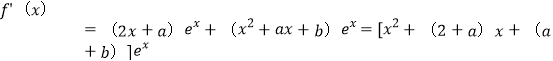
當![]() ,
,![]() 時,
時,![]() 則
則![]()
令![]() 得
得![]() ,∵
,∵![]() ∴
∴![]() ,解得
,解得![]() ,
,![]()
∵當![]() 時,
時,![]() ,當
,當![]() 時
時![]() ,當
,當![]() 時
時![]()
∴當![]() 時,函數
時,函數![]() 有極大值,
有極大值,![]() ,
,
當![]() 時,函數
時,函數![]() 有極小值,
有極小值,![]() .
.
(2)由(1)知![]()
∵![]() 是函數
是函數![]() 的一個極值點
的一個極值點
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
則![]()
令![]() ,得
,得![]() 或
或![]()
∵![]() 是極值點,∴
是極值點,∴![]() ,即
,即![]()
當![]() 即
即![]() 時,由
時,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
當![]() 即
即![]() 時,由
時,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
綜上可知:當![]() 時,單調遞增區間為
時,單調遞增區間為![]() 和
和![]() ,遞減區間為
,遞減區間為![]()
當![]() 時,單調遞增區間為
時,單調遞增區間為![]() 和
和![]() ,遞減區間為
,遞減區間為![]()
(3)由(2)知,當![]() 時,
時,![]() 在區間
在區間![]() 上的單調遞減,在區間
上的單調遞減,在區間![]() 上單調遞增,
上單調遞增,
∴函數![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]()
又∵![]() ,
,![]() ,
,
∴函數![]() 在區間
在區間![]() 上的值域是
上的值域是![]() ,即
,即![]()
又![]() 在區間
在區間![]() 上是增函數,
上是增函數,
且它在區間![]() 上的值域是
上的值域是![]()
∵![]() ,
,
∴存在![]() 使得
使得![]()
成立只須僅須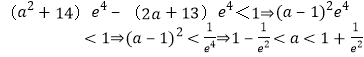 .
.


科目:高中數學 來源: 題型:
【題目】某學校高二年級的第二學期,因某學科的任課教師王老師調動工作,于是更換了另一名教師趙老師繼任.第二學期結束后從全學年的該門課的學生考試成績中用隨機抽樣的方法抽取了容量為50的樣本,用莖葉圖表示如下:
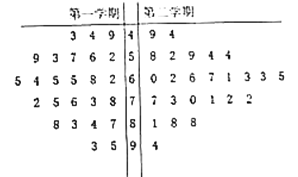
學校秉持均衡發展、素質教育的辦學理念,對教師的教學成績實行績效考核,績效考核方案規定:每個學期的學生成績中與其中位數相差在![]() 范圍內(含
范圍內(含![]() )的為合格,此時相應的給教師賦分為1分;與中位數之差大于10的為優秀,此時相應的給教師賦分為2分;與中位數之差小于-10的為不合格,此時相應的給教師賦分為-1分.
)的為合格,此時相應的給教師賦分為1分;與中位數之差大于10的為優秀,此時相應的給教師賦分為2分;與中位數之差小于-10的為不合格,此時相應的給教師賦分為-1分.
(Ⅰ)問王老師和趙老師的教學績效考核平均成績哪個大?
(Ⅱ)是否有![]() 的把握認為“學生成績取得優秀與更換老師有關”.
的把握認為“學生成績取得優秀與更換老師有關”.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2019年的冬令營考試成績中隨機抽取100名學生的筆試成績,按成績分組,得到的頻率分布表如下圖所示:
組號 | 分組 | 頻數 | 頻率 |
第1組 |
| 5 | 0.050 |
第2組 |
| 35 | 0.350 |
第3組 |
| 10 | 0.100 |
第4組 |
| 20 | 0.200 |
第5組 |
| 30 | 0.300 |
合計 | 100 | 1.00 | |
(1)為了能選拔出最優秀的學生,高校決定在筆試成績高的第3、4、5組中用分層抽樣抽取6名學生進入第二輪面試,求第3、4、5組每組各抽取多少名學生進入第二輪面試?
(2)在(1)的前提下,高校決定在這6名學生中,隨機抽取2名學生接受A考官進行面試,求第4組至少有一名學生被A考官測試的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,已知![]() ,且2an+1=an+1(n∈N*).
,且2an+1=an+1(n∈N*).
(1)求證:數列{an-1}是等比數列;
(2)若bn=nan,求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,楔形幾何體![]() 由一個三棱柱截去部分后所得,底面
由一個三棱柱截去部分后所得,底面![]() 側面
側面![]() ,
,![]() ,楔面
,楔面![]() 是邊長為2的正三角形,點
是邊長為2的正三角形,點![]() 在側面
在側面![]() 的射影是矩形
的射影是矩形![]() 的中心
的中心![]() ,點
,點![]() 在
在![]() 上,且
上,且![]()
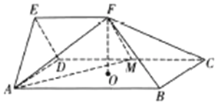
(1)證明:![]() 平面
平面![]() ;
;
(2)求楔面![]() 與側面
與側面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知如圖,長方體![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 的中點,過點
的中點,過點![]() 的平面
的平面![]() 與平面
與平面![]() 平行,且與長方體的面相交,交線圍成一個幾何圖形.
平行,且與長方體的面相交,交線圍成一個幾何圖形.
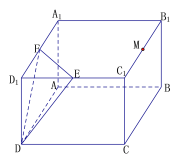
(1)在圖中畫出這個幾何圖形,并求這個幾何圖形的面積(畫圖說出作法,不用說明理由);
(2)求證:![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com