
【題目】如圖,已知四棱錐![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() .
.
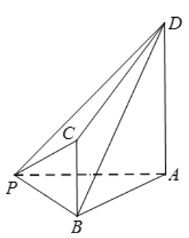
(1)證明:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)分別取![]() ,
,![]() 的中點
的中點![]() ,
,![]() ,連結
,連結![]() ,
,![]() ,
,![]() ,要證
,要證![]() 平面
平面![]() ,需證明
,需證明![]() ,
,![]() ,其中可通過證明
,其中可通過證明![]() 平面
平面![]() 來證明
來證明![]() ,通過證明
,通過證明![]() 平面
平面![]() 來證明
來證明![]() ;
;
(2)以A為坐標原點,建立空間直角坐標系,求出面![]() 的一個法向量以及直線
的一個法向量以及直線![]() 的方向向量,求出兩向量的夾角的余弦值即為直線
的方向向量,求出兩向量的夾角的余弦值即為直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
(1)證明:分別取![]() ,
,![]() 的中點
的中點![]() ,
,![]() ,連結
,連結![]() ,
,![]() ,
,![]() .
.
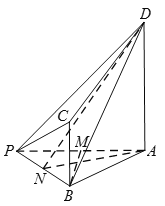
因![]() ,
,![]() 為
為![]() 的中點,
的中點,
故![]() .
.
同理,![]() ,
,![]() .
.
故![]() 平面
平面![]() .
.
故![]() .
.
因平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
故![]() 平面
平面![]() .
.
則![]() .
.
又![]() ,
,![]() 是平面
是平面![]() 中的相交直線,
中的相交直線,
故![]() 平面
平面![]() .
.
(2)由(1)知,![]() 面
面![]() ,又
,又![]() ∥
∥![]() ,
,
![]() 面
面![]() .
.
如圖,以A為坐標原點,建立空間直角坐標系,
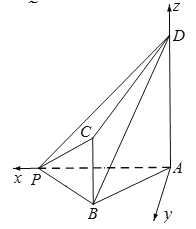
不妨設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]() .
.
設![]() 是面
是面![]() 的一個法向量,
的一個法向量,
則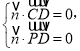 ,即
,即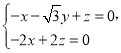 ,
,
取![]() ,則
,則![]() .
.
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則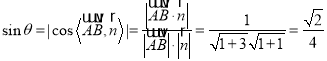 ,
,
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ;直線
;直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() ,
,![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若點![]() 的極坐標為
的極坐標為![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 做斜率為
做斜率為![]() 的直線
的直線![]() ,橢圓
,橢圓![]() 與直線
與直線![]() 交于
交于![]() 兩點,當直線
兩點,當直線![]() 垂直于
垂直于![]() 軸時
軸時![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當![]() 變化時,在
變化時,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為底的等腰三角形,若存在求出
為底的等腰三角形,若存在求出![]() 的取值范圍,若不存在說明理由.
的取值范圍,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為零的等差數列{an}滿足:a3+a8=20,且a5是a2與a14的等比中項.
(1)求數列{an}的通項公式;
(2)設數列{bn}滿足![]() ,求數列{bn}的前n項和Sn.
,求數列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】業界稱“中國芯”迎來發展和投資元年,某芯片企業準備研發一款產品,研發啟動時投入資金為![]() (
(![]() 為常數)元,之后每年會投入一筆研發資金,
為常數)元,之后每年會投入一筆研發資金,![]() 年后總投入資金記為
年后總投入資金記為![]() ,經計算發現當
,經計算發現當![]() 時,
時,![]() 近似地滿足
近似地滿足![]() ,其中
,其中![]() 為常數,
為常數,![]() .已知
.已知![]() 年后總投入資金為研發啟動時投入資金的
年后總投入資金為研發啟動時投入資金的![]() 倍.問
倍.問
(1)研發啟動多少年后,總投入資金是研發啟動時投入資金的![]() 倍;
倍;
(2)研發啟動后第幾年的投入資金的最多.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在區間
,若存在區間![]() ,使得
,使得![]() ,則稱函數
,則稱函數![]() 為“可等域函數”,區間
為“可等域函數”,區間![]() 為函數的一個“可等域區間”.給出下列四個函數:
為函數的一個“可等域區間”.給出下列四個函數:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中存在唯一“可等域區間”的“可等域函數”的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,OM,ON是兩條海岸線,Q為海中一個小島,A為海岸線OM上的一個碼頭.已知![]() ,
,![]() ,Q到海岸線OM,ON的距離分別為3 km,
,Q到海岸線OM,ON的距離分別為3 km,![]() km.現要在海岸線ON上再建一個碼頭,使得在水上旅游直線AB經過小島Q.
km.現要在海岸線ON上再建一個碼頭,使得在水上旅游直線AB經過小島Q.
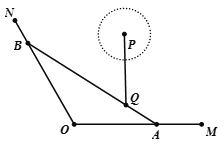
(1)求水上旅游線AB的長;
(2)若小島正北方向距離小島6 km處的海中有一個圓形強水波P,從水波生成t h時的半徑為![]() (a為大于零的常數).強水波開始生成時,一游輪以
(a為大于零的常數).強水波開始生成時,一游輪以![]() km/h的速度自碼頭A開往碼頭B,問實數a在什么范圍取值時,強水波不會波及游輪的航行.
km/h的速度自碼頭A開往碼頭B,問實數a在什么范圍取值時,強水波不會波及游輪的航行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S-ABCD中,四邊形ABCD菱形,![]() ,平面
,平面![]() 平面 ABCD,
平面 ABCD,![]() .E,F 分別是線段 SC,AB 上的一點,
.E,F 分別是線段 SC,AB 上的一點, ![]() .
.
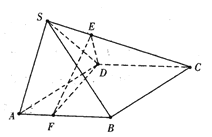
(1)求證:![]() 平面SAD;
平面SAD;
(2)求平面DEF與平面SBC所成銳二面角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com