
已知E、F、G、H分別是空間四邊形ABCD的邊AB、BC、CD、DA的中點,
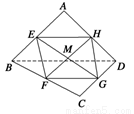
(1)求證:E、F、G、H四點共面;
(2)求證:BD∥平面EFGH;
(3)設M是EG和FH的交點,求證:對空間任一點O,有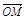 =
= (
( +
+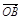 +
+ +
+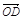 ).
).
 證明 見解析。
證明 見解析。
【解析】
試題分析: 證明 (1)連接BG,則
證明 (1)連接BG,則
 =
= +
+
= +
+ (
( +
+ )
)
=  +
+ +
+ =
= +
+ ,
,
由共面向量定理的推論知:
E、F、G、H四點共面.
(2)因為 =
= -
-
=
 -
-
 =
= (
( -
- )=
)=
 ,
,
所以EH∥BD.
又EH 平面EFGH,
平面EFGH,
BD 平面EFGH,
平面EFGH,
所以BD∥平面EFGH.
(3)連接OM,OA,OB,OC,OD,OE,OG.
由(2)知 =
=
 ,
,
同理 =
=
 ,
,
 所以
所以 =
= ,即EH FG,
,即EH FG,
所以四邊形EFGH是平行四邊形.
所以EG,FH交于一點M且被M平分.
故 =
= (
( +
+ )=
)=
 +
+

= [
[ (
( +
+ )]+
)]+ [
[ (
( +
+ )]
)]
= (
( +
+ +
+ +
+ ).
).
考點:本題主要考查共線向量與共面向量,向量的應用。
點評:用向量語言表述線面的垂直、平行關系,考查運算能力,是中檔題。


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
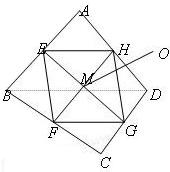 已知E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA的中點.
已知E,F,G,H分別是空間四邊形ABCD的邊AB,BC,CD,DA的中點.| OM |
| 1 |
| 4 |
| OA |
| OB |
| OC |
| OD |
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)用向量法證明E、F、G、H四點共面;
(2)用向量法證明BD∥平面EFGH.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com