
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若函數![]() 在區間
在區間![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)設![]() 是函數
是函數![]() 圖象上任意不同的兩點,線段
圖象上任意不同的兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,證明:
,證明:![]() .
.
【答案】(1)函數![]() 的單調增區間是
的單調增區間是![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
試題(1)求出![]() 的導數,導數大于
的導數,導數大于![]() ,即可求函數的增區間;
,即可求函數的增區間;
(2)對![]() 進行分類討論,分別求出各種情況下的函數在
進行分類討論,分別求出各種情況下的函數在![]() 上的最小值令其為
上的最小值令其為![]() ,解方程求得
,解方程求得![]() 的值;
的值;
(3)對于當![]() 時,先把
時,先把![]() 具體出來,然后求導函數,得到
具體出來,然后求導函數,得到![]() ,在利用斜率公式求出過這兩點的斜率公式,利用構造函數并利用構造函數的單調性比較大小.
,在利用斜率公式求出過這兩點的斜率公式,利用構造函數并利用構造函數的單調性比較大小.
試題解析: (1)解:![]() ,則
,則![]() ,
,![]() ,
,
∴函數![]() 的單調增區間是
的單調增區間是![]() ;
;
(2)解:在![]() 上,分如下情況討論:
上,分如下情況討論:
1.當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增,其最小值為
單調遞增,其最小值為![]() ,這與函數在
,這與函數在![]() 上的最小值是
上的最小值是![]() 相矛盾;
相矛盾;
2.當![]() 時,函數
時,函數![]() 在
在![]() 單調遞增,其最小值為
單調遞增,其最小值為![]() ,同樣與最小值是
,同樣與最小值是![]() 相矛盾;
相矛盾;
3.當![]() 時,函數
時,函數![]() 在
在![]() 上有
上有![]() ,單調遞減,在
,單調遞減,在![]() 上有
上有![]() ,單調遞增,
,單調遞增,
∴函數![]() 的最小值為
的最小值為![]() ,得
,得![]() .
.
4.當![]() 時,函數
時,函數![]() 在
在![]() 上有
上有![]() ,單調遞減,其最小值為
,單調遞減,其最小值為![]() ,與最小值是
,與最小值是![]() 相矛盾;
相矛盾;
5.當![]() 時,顯然函數
時,顯然函數![]() 在
在![]() 上單調遞減,其最小值為
上單調遞減,其最小值為![]() ,與最小值是
,與最小值是![]() 相矛盾.
相矛盾.
綜上所述,![]() 的值為
的值為![]() .
.
(3)證明:當![]() 時,
時,![]() ,
,![]()
又 ,不妨設
,不妨設![]() ,要比較
,要比較![]() 與
與![]() 的大小,
的大小,
即比較![]() 與
與![]() 的大小,又因為
的大小,又因為![]() ,
,
所以即比較![]() 與
與 的大小.
的大小.
令![]() ,則
,則![]() ∴
∴![]() 在
在![]() 上是增函數.
上是增函數.
又![]() ,∴
,∴![]() ,
, ,即
,即![]() .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】隨著資本市場的強勢進入,互聯網共享單車“忽如一夜春風來”,遍布了一二線城市的大街小巷.為了解共享單車在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了200人進行抽樣分析,得到下表(單位:人):
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了200人進行抽樣分析,得到下表(單位:人):
經常使用 | 偶爾或不用 | 合計 | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據以上數據,能否在犯錯誤的概率不超過0.15的前提下認為![]() 市使用共享單車情況與年齡有關?
市使用共享單車情況與年齡有關?
(2)現從所有抽取的30歲以上的網民中利用分層抽樣抽取5人,
![]() 求這5人中經常使用、偶爾或不用共享單車的人數;
求這5人中經常使用、偶爾或不用共享單車的人數;
![]() 從這5人中,在隨機選出2人贈送一件禮品,求選出的2人中至少有1人經常使用共享單車的概率.
從這5人中,在隨機選出2人贈送一件禮品,求選出的2人中至少有1人經常使用共享單車的概率.
參考公式: 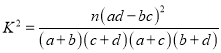 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一盒中裝有12個球,其中5個紅球,4個黑球,2個白球,1個綠球.從中隨機取出1球,求:
(1)取出1球是紅球或黑球的概率;
(2)取出1球是紅球或黑球或白球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自由購是通過自助結算方式購物的一種形式. 某大型超市為調查顧客使用自由購的情況,隨機抽取了100人,統計結果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人數 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人數 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)現隨機抽取 1 名顧客,試估計該顧客年齡在![]() 且未使用自由購的概率;
且未使用自由購的概率;
(Ⅱ)從被抽取的年齡在![]() 使用自由購的顧客中,隨機抽取3人進一步了解情況,用
使用自由購的顧客中,隨機抽取3人進一步了解情況,用![]() 表示這3人中年齡在
表示這3人中年齡在![]() 的人數,求隨機變量
的人數,求隨機變量![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅲ)為鼓勵顧客使用自由購,該超市擬對使用自由購的顧客贈送1個環保購物袋.若某日該超市預計有5000人購物,試估計該超市當天至少應準備多少個環保購物袋.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】精準扶貧是鞏固溫飽成果、加快脫貧致富、實現中華民族偉大“中國夢”的重要保障.某地政府在對某鄉鎮企業實施精準扶貧的工作中,準備投入資金將當地農產品進行二次加工后進行推廣促銷,預計該批產品銷售量![]() 萬件(生產量與銷售量相等)與推廣促銷費
萬件(生產量與銷售量相等)與推廣促銷費![]() 萬元之間的函數關系為
萬元之間的函數關系為![]() (其中推廣促銷費不能超過5千元).已知加工此農產品還要投入成本
(其中推廣促銷費不能超過5千元).已知加工此農產品還要投入成本![]() 萬元(不包括推廣促銷費用),若加工后的每件成品的銷售價格定為
萬元(不包括推廣促銷費用),若加工后的每件成品的銷售價格定為![]() 元/件.
元/件.
(1)試將該批產品的利潤![]() 萬元表示為推廣促銷費
萬元表示為推廣促銷費![]() 萬元的函數;(利潤=銷售額-成本-推廣促銷費)
萬元的函數;(利潤=銷售額-成本-推廣促銷費)
(2)當推廣促銷費投入多少萬元時,此批產品的利潤最大?最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個三棱錐的三個側面中有兩個是等腰直角三角形, 另一個是邊長為 1 的正三角形.那么, 這個三棱錐的體積大小 ( ).
A. 有惟一確定的值 B. 有 2 個不同值
C. 有 3 個不同值 D. 有 3 個以上不同值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓E:
中,已知橢圓E:![]() (
(![]() )過點
)過點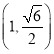 ,其心率等于
,其心率等于![]() .
.
(1)求橢圓E的標準方程;
(2)若A,B分別是橢圓E的左,右頂點,動點M滿足![]() ,且
,且![]() 橢圓E于點P.
橢圓E于點P.
①求證:![]() 為定值:
為定值:
②設![]() 與以
與以![]() 為直徑的圓的另一交點為Q,求證:直線
為直徑的圓的另一交點為Q,求證:直線![]() 經過定點.
經過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com