
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若對于任意![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)在(0,1)上 ![]() 單調遞減,在(1,+∞)上
單調遞減,在(1,+∞)上![]() 單調遞增;(2)
單調遞增;(2) ![]()
【解析】試題分析:(1)求導得到區間![]() 上
上![]() 單調遞減,
單調遞減, ![]() 上
上![]() 單調遞增;(2)直接求導,對
單調遞增;(2)直接求導,對![]() 分類討論,得到
分類討論,得到![]() .
.
試題解析:
(1)![]() ,令其為
,令其為![]() ,則
,則![]() 所以可得
所以可得![]()
即![]() 單調遞增,
單調遞增,
而![]() ,則在區間
,則在區間![]() 上,
上, ![]() ,函數
,函數![]() 單調遞減;
單調遞減;
在區間![]() 上
上![]() ,函數
,函數![]() 單調遞增
單調遞增
(2)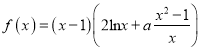 ,另
,另![]() ,可知
,可知![]() .
.
![]() ,令
,令![]() ,
,
①當![]() 時,結合
時,結合![]() 對應二次函數的圖像可知,
對應二次函數的圖像可知, ![]() ,即
,即![]() ,所以
,所以
函數![]() 單調遞減,∵
單調遞減,∵ ![]() ,∴
,∴ ![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() .
.
可知此時![]() 滿足條件.
滿足條件.
②當![]() 時,結合
時,結合![]() 對應二次函數的圖像可知,
對應二次函數的圖像可知, ![]() ,
, ![]() 單調遞增,
單調遞增,
∵![]() ,∴
,∴![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() .可知此時
.可知此時![]() 不成立.
不成立.
③當![]() 時,研究函數
時,研究函數![]() .可知
.可知![]() .對稱軸
.對稱軸![]() .
.
那么![]() 在區間
在區間![]() 大于0,即
大于0,即![]() 在區間
在區間![]() 大于0,
大于0, ![]() 在區間
在區間![]() 單調遞增,
單調遞增, ![]() ,可知此時
,可知此時![]() .所以不滿足條件.
.所以不滿足條件.
綜上所述: ![]() .
.


科目:高中數學 來源: 題型:
【題目】某地最近出臺一項機動車駕照考試規定:每位考試者一年之內最多有4次參加考試的機會,一旦某次考試通過,便可領取駕照,不再參加以后的考試,否則就一直考到第4次為止.如果李明決定參加駕照考試,設他每次參加考試通過的概率依次為0.6, 0.7, 0.8, 0.9.
(1)求在一年內李明參加駕照考試次數![]() 的分布列和數學期望;
的分布列和數學期望;
(2)求李明在一年內領到駕照的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)當m=-1時,求A∪B;
(2)若AB,求實數m的取值范圍;
(3)若A∩B=,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著網絡的發展,網上購物越來越受到人們的喜愛,各大購物網站為增加收入,促銷策略越來越多樣化,促銷費用也不斷增加.下表是某購物網站2017年1-8月促銷費用(萬元)和產品銷量(萬件)的具體數據.

(1)根據數據繪制的散點圖能夠看出可用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數
的關系,請用相關系數![]() 加以說明;(系數精確到0.001)
加以說明;(系數精確到0.001)
(2)建立![]() 關于
關于![]() 的回歸方程
的回歸方程![]() (系數精確到0.01);如果該公司計劃在9月份實現產品銷量超6萬件,預測至少需投入促銷費用多少萬元(結果精確到0.01).
(系數精確到0.01);如果該公司計劃在9月份實現產品銷量超6萬件,預測至少需投入促銷費用多少萬元(結果精確到0.01).
參考數據: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分別為第
分別為第![]() 個月的促銷費用和產品銷量,
個月的促銷費用和產品銷量, ![]() .
.
參考公式:(1)樣本![]() 的相關系數
的相關系數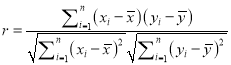
(2)對于一組數據![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為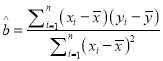 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)設![]() ,求證:數列
,求證:數列![]() 是等差數列,并求出
是等差數列,并求出![]() 的通項公式;
的通項公式;
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,是否存在正整數
,是否存在正整數![]() ,使得
,使得![]() 對于
對于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,請說明理由.
的最小值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=excos x-x.
(1)求曲線y=f(x)在點(0,f(0))處的切線方程;
(2)求函數f(x)在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com