
【題目】已知函數![]() .
.
(Ⅰ)已知![]() 是
是![]() 的一個極值點,求曲線
的一個極值點,求曲線![]() 在
在![]() 處的切線方程
處的切線方程
(Ⅱ)討論關于![]() 的方程
的方程![]() 根的個數.
根的個數.
【答案】(Ⅰ)![]() ;(Ⅱ)見解析
;(Ⅱ)見解析
【解析】
(Ⅰ)求函數的導數,利用x=2是f (x)的一個極值點,得f' (2) =0建立方程求出a的值,結合導數的幾何意義進行求解即可;
(Ⅱ)利用參數法分離法得到![]() ,構造函數求出函數的導數研究函數的單調性和最值,利用數形結合轉化為圖象交點個數進行求解即可.
,構造函數求出函數的導數研究函數的單調性和最值,利用數形結合轉化為圖象交點個數進行求解即可.
(Ⅰ)因為![]() ,則
,則![]() ,
,
因為![]() 是
是![]() 的一個極值點,所以
的一個極值點,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
因為![]() ,
,![]() ,
,
則直線方程為![]() ,即
,即![]() ;
;
(Ⅱ)因為![]() ,所以
,所以![]() ,
,
所以![]() ,設
,設![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數,
上是減函數,
故![]() ,
,
所以![]() ,所以
,所以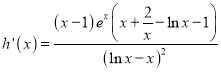 ,
,
設![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上是減函數,
上是減函數,![]() 上是增函數,
上是增函數,
所以![]() ,
,
所以當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 是減函數,
是減函數,
當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 是增函數,
是增函數,
因為![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
所以當![]() 時,方程無實數根,
時,方程無實數根,
當![]() 時,方程有兩個不相等實數根,
時,方程有兩個不相等實數根,
當![]() 或
或![]() 時,方程有1個實根.
時,方程有1個實根.


科目:高中數學 來源: 題型:
【題目】2019年4月25日-27日,北京召開第二屆“一帶一路”國際高峰論壇,組委會要從6個國內媒體團和3個國外媒體團中選出3個媒體團進行提問,要求這三個媒體團中既有國內媒體團又有國外媒體團,且國內媒體團不能連續提問,則不同的提問方式的種數為 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為定義域R上的奇函數,且在R上是單調遞增函數,函數
為定義域R上的奇函數,且在R上是單調遞增函數,函數![]() ,數列
,數列![]() 為等差數列,且公差不為0,若
為等差數列,且公差不為0,若![]() ,則
,則![]() ( )
( )
A. 45B. 15C. 10D. 0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓過定點![]() ,且與直線l:
,且與直線l:![]() 相切.
相切.
(1)求動圓圓心的軌跡C的方程;
(2)過F作斜率為![]() 的直線m與C交于兩點A,B,過A,B分別作C的切線,兩切線交點為P,證明:點P始終在直線l上且
的直線m與C交于兩點A,B,過A,B分別作C的切線,兩切線交點為P,證明:點P始終在直線l上且![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com