
【題目】函數![]() ,其中
,其中![]() ,
,![]() ,為實常數
,為實常數
(1)若![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(2)若![]() 時,不等式
時,不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,當
,當![]() 時,證明:
時,證明:![]() .
.
【答案】(1)見解析;(2) ![]() (3)見證明
(3)見證明
【解析】
(1)代入t的值,求得導函數,對a進行分類討論,根據導數的正負確定單調區間即可.
(2)代入t的值,根據不等式分離參數,通過構造函數![]() ,再求
,再求![]() ,根據其單調性求得最大值即可得a的取值范圍.
,根據其單調性求得最大值即可得a的取值范圍.
(3)要證明不等式成立,根據分析法得到只需證明![]() 成立即可.通過構造函數
成立即可.通過構造函數![]() ,利用導數研究其單調性與最值,根據最小值即可得證.
,利用導數研究其單調性與最值,根據最小值即可得證.
解(1)定義域為![]() ,
,![]()
![]() ,
,
當![]() 時,
時,![]() ,
,![]()
![]() ,
,
![]() 在定義域
在定義域![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() .
.![]() 單調遞減;
單調遞減;
綜上可知:當![]() 時,
時,![]() 的增區間為
的增區間為![]() ,無減區間;
,無減區間;
當![]() 時,增區間為
時,增區間為![]() ,減區間為
,減區間為![]() ;
;
(2)![]()
![]()
![]()
![]() 對任意
對任意![]() 恒成立.
恒成立.
即等價于![]() ,
,![]() ,
,
令![]() .
.
![]()
![]() ,
,![]() ,
,
![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,
![]() .故
.故![]() 的取值范圍為
的取值范圍為![]() .
.
(3)要證明![]() ,即證明
,即證明![]() ,只要證
,只要證![]() ,
,
即證![]() ,只要證明
,只要證明![]() 即可,
即可,
令![]() ,
,![]() 在
在![]() 上是單調遞增,
上是單調遞增,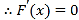 ,
,
![]() 在
在![]() 有唯一實根設為
有唯一實根設為![]() ,
,
且![]() ,
,
當![]() 時
時![]() ,
,![]() 單調遞減
單調遞減
當![]() 時,
時,![]() ,
,![]() 單調遞增
單調遞增
從而當![]() 時,
時,![]() 取得最小值,由
取得最小值,由![]() 得:
得:
![]() ,即
,即![]() ,
,
![]()
![]()
![]()
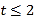 ,
,
故當![]() 時,證得:
時,證得:![]() .
.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為等邊三角形,且點P在底面
為等邊三角形,且點P在底面![]() 上的射影為
上的射影為![]() 的中點G,點E在線段
的中點G,點E在線段![]() 上,且
上,且![]() .
.
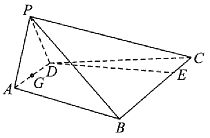
(1)求證:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在P地正西方向16km的A處和正東方向2km的B處各一條正北方向的公路AC和BD,現計劃在AC和BD路邊各修建一個物流中心E和F.
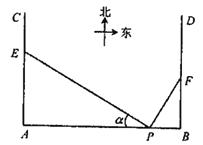
(1)若在P處看E,F的視角![]() ,在B處看E測得
,在B處看E測得![]() ,求AE,BF;
,求AE,BF;
(2)為緩解交通壓力,決定修建兩條互相垂直的公路PE和PF,設![]() ,公路PF的毎千米建設成本為a萬元,公路PE的毎千米建設成本為8a萬元.為節省建設成本,試確定E,F的位置,使公路的總建設成本最小.
,公路PF的毎千米建設成本為a萬元,公路PE的毎千米建設成本為8a萬元.為節省建設成本,試確定E,F的位置,使公路的總建設成本最小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com