
如圖,在四棱錐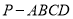 中,底面
中,底面 是菱形,
是菱形,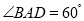 ,
,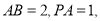
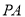
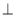 平面
平面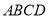 ,點
,點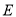 是
是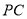 的中點,
的中點,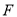 是
是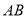 的中點.
的中點.

(Ⅰ)求證: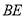 ∥平面
∥平面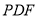 ;
;
(Ⅱ)求直線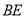 與平面
與平面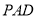 所成角的正弦值.
所成角的正弦值.
(1)證明見解析;(2) .
.
【解析】
試題分析:(1)利用線面平行的判定進行證明;(2)利用線面垂直找出線面角,再構造三角形進行求角.
解題思路:求直線與平面所成角的一般步驟:(1)找出或證明線面垂直,(2)證角;(3)求角.
試題解析:(1)證明: 取 中點為
中點為 ,連
,連
∵ 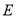 是
是 的中點 ∴
的中點 ∴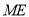 是
是 的中位線,∴
的中位線,∴ 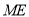
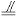
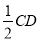
∵  是
是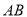 中點且
中點且 是菱形,
是菱形,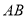
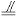
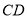 ,∴
,∴ 
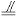
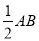 . ∴
. ∴ 
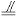
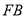
∴ 四邊形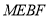 是平行四邊形. 從而
是平行四邊形. 從而 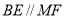 ,
,
∵ 
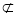 平面
平面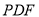 ,
,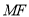
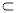 平面
平面 ,
,
∴ 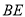 ∥平面
∥平面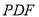
(Ⅱ)【解析】
由(Ⅰ)得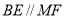 ,
,
∴直線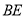 與平面
與平面 所成角就是直線
所成角就是直線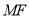 與平面
與平面 所成角。
所成角。
過 作
作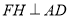 ,垂足為
,垂足為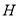 ,連
,連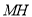
∵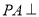 平面
平面 ∴面
∴面 平面
平面
又∵面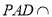 平面
平面 =
=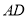 ,
,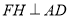 ∴
∴
∴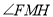 是直線
是直線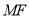 與平面
與平面 所成的線面角
所成的線面角
又底面 是菱形,
是菱形,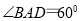 ,
,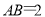 ,
, 是
是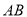 的中點∴
的中點∴ ,
,
又∵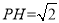 ,
,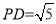 ∴
∴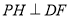 ∴
∴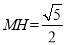 ,
,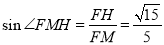 .
.
∴直線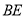 與平面
與平面 所成的線面角的正弦值為
所成的線面角的正弦值為 .
.
考點:1.空間中平行關系的轉化;2.直線與平面所成的角.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
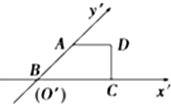 有一塊多邊形的菜地,它的水平放置的平面圖形的斜二測直觀圖是直角梯形(如圖),AD=DC=1,DC⊥BC,則這塊菜地的面積( )
有一塊多邊形的菜地,它的水平放置的平面圖形的斜二測直觀圖是直角梯形(如圖),AD=DC=1,DC⊥BC,則這塊菜地的面積( )A、
| ||||
B、3
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中數學 來源:2014-2015學年甘肅省高二上學期第四次月考理科數學試卷(解析版) 題型:選擇題
已知雙曲線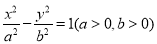 與拋物線
與拋物線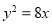 有一個公共的焦點
有一個公共的焦點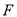 ,且兩曲線的一個交點為
,且兩曲線的一個交點為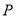 ,若
,若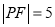 ,則雙曲線的漸近線方程為( )
,則雙曲線的漸近線方程為( )
(A)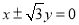
(B)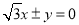
(C)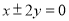
(D)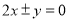
查看答案和解析>>
科目:高中數學 來源:[同步]2014年湘教版選修2-3 8.4列聯表獨立性分析案例練習卷(解析版) 題型:?????
(2013•江西一模)甲、乙兩名棋手比賽正在進行中,甲必須再勝2盤才最后獲勝,乙必須再勝3盤才最后獲勝,若甲、乙兩人每盤取勝的概率都是 ,則甲最后獲勝的概率是( )
,則甲最后獲勝的概率是( )
A.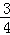 B.
B.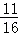 C.
C.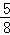 D.
D.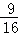
查看答案和解析>>
科目:高中數學 來源:[同步]2014年湘教版選修2-1 3.9共面與平行練習卷(解析版) 題型:?????
已知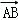 =(1,5,﹣2),
=(1,5,﹣2),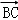 =(3,1,z),若
=(3,1,z),若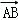 ⊥
⊥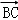 ,
,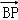 =(x﹣1,y,﹣3),且BP⊥平面ABC,則實數x、y、z分別為( )
=(x﹣1,y,﹣3),且BP⊥平面ABC,則實數x、y、z分別為( )
A.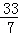 ,﹣
,﹣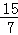 ,4 B.
,4 B.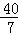 ,﹣
,﹣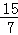 ,4 C.
,4 C.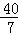 ,﹣2,4 D.4,
,﹣2,4 D.4,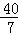 ,﹣15
,﹣15
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com