
【題目】已知函數f(x)=|2x﹣a|+a.
(Ⅰ)若不等式f(x)≤6的解集為{x|﹣2≤x≤3},求實數a的值;
(Ⅱ)在(Ⅰ)的條件下,若存在實數n使f(n)≤m﹣f(﹣n)成立,求實數m的取值范圍.
【答案】解:(Ⅰ)∵函數f(x)=|2x﹣a|+a,故不等式f(x)≤6,即 ![]() ,求得 a﹣3≤x≤3.
,求得 a﹣3≤x≤3.
再根據不等式的解集為{x|﹣2≤x≤3},可得a﹣3=﹣2,∴實數a=1.
(Ⅱ)在(Ⅰ)的條件下,f(x)=|2x﹣1|+1,∴f(n)=|2n﹣1|+1,存在實數n使f(n)≤m﹣f(﹣n)成立,
即f(n)+f(﹣n)≤m,即|2n﹣1|+|2n+1|+2≤m.
由于|2n﹣1|+|2n+1|≥|(2n﹣1)﹣(2n+1)|=2,∴|2n﹣1|+|2n+1|的最小值為2,∴m≥4,
故實數m的取值范圍是[4,+∞)
【解析】(Ⅰ)不等式f(x)≤6,即 ![]() ,求得a﹣3≤x≤3.再根據不等式的解集為{x|﹣2≤x≤3},可得a﹣3=﹣2,從而求得實數a的值.(Ⅱ)在(Ⅰ)的條件下,f(n)=|2n﹣1|+1,即f(n)+f(﹣n)≤m,即|2n﹣1|+|2n+1|+2≤m.求得|2n﹣1|+|2n+1|的最小值為2,可得m的范圍.
,求得a﹣3≤x≤3.再根據不等式的解集為{x|﹣2≤x≤3},可得a﹣3=﹣2,從而求得實數a的值.(Ⅱ)在(Ⅰ)的條件下,f(n)=|2n﹣1|+1,即f(n)+f(﹣n)≤m,即|2n﹣1|+|2n+1|+2≤m.求得|2n﹣1|+|2n+1|的最小值為2,可得m的范圍.


科目:高中數學 來源: 題型:
【題目】某校高三年級進行了一次學業水平測試,用系統抽樣的方法抽取了50名學生的數學成績,準備進行分析和研究.經統計,成績的分組及各組的頻數如下: ![]() ,2;
,2; ![]() ,3;
,3; ![]() ,10;
,10; ![]()
15; ![]() ,12;
,12; ![]() ,8.
,8.
(1)完成樣本的頻率分布表,畫出頻率分布直方圖;
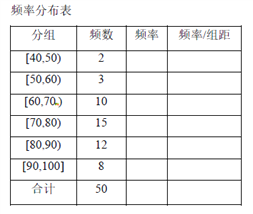
(2)估計成績在85分以下的學生比例;
(3)請你根據以上信息去估計樣本的眾數、中位數、平均數(精確到0.01).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,設圓x2+y2-4x=0的圓心為Q.
(1)求過點P(0,-4)且與圓Q相切的直線的方程;
(2)若過點p(0,-4)且斜率為k的直線與圓Q相交于不同的兩點A,B,以OA、OB為鄰邊做平行四邊形OABC,問是否存在常數k,使得平行四邊形OABC為矩形?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是各項均為正數的等比數列,{bn}是等差數列,且a1=b1=1,b2+b3=2a3,a5-3b2=7.
(Ⅰ)求{an}和{bn}的通項公式;
(Ⅱ)設![]() ,n∈N*,求數列{cn}的前n項和.
,n∈N*,求數列{cn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,A,B,C成等差數列是(b+a﹣c)(b﹣a+c)=ac的( )
A.充分但不必要條件
B.必要但不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,PA⊥平面ABCD,四邊形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2,AB=2 ![]() .
. 
(1)求異面直線PC與AD所成角的大小;
(2)若平面ABCD內有一經過點C的曲線E,該曲線上的任一動點Q都滿足PQ與AD所成角的大小恰等于PC與AD所成角.試判斷曲線E的形狀并說明理由;
(3)在平面ABCD內,設點Q是(2)題中的曲線E在直角梯形ABCD內部(包括邊界)的一段曲線CG上的動點,其中G為曲線E和DC的交點.以B為圓心,BQ為半徑r的圓分別與梯形的邊AB、BC交于M、N兩點.當Q點在曲線段CG上運動時,試求圓半徑r的范圍及VP﹣BMN的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農科院的專家為了了解新培育的甲、乙兩種麥苗的長勢情況,從甲、乙兩種麥苗的試驗田中各抽取6株麥苗測量麥苗的株高,數據如下:(單位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在給出的方框內繪出所抽取的甲、乙兩種麥苗株高的莖葉圖;
(2)分別計算所抽取的甲、乙兩種麥苗株高的平均數與方差,并由此判斷甲、乙兩種麥苗的長勢情況.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com