已知函數(shù)

為常數(shù),e=2.71828…是自然對數(shù)的底數(shù)),曲線

在點

處的切線與x軸平行.
(1)求k的值,并求

的單調區(qū)間;
(2)設

,其中

為

的導函數(shù).證明:對任意

.
(1)

,

的單調遞增區(qū)間是

,單調遞減區(qū)間是

;(2)證明過程見試題解析.
試題分析:(1)利用在

處的導數(shù)為0,可求k,進而再利用導函數(shù)求出

的單調區(qū)間;(2)由(1)易證不等式在

時成立,只需證

時,又

,易證

最大值為

,則對任意

.
(1)

,
由已知,

,∴

.
由

,
設

,則

,即

在

上是減函數(shù),
由

知,當

時

,從而

,
當

時

,從而

.
綜上可知,

的單調遞增區(qū)間是

,單調遞減區(qū)間是

.
(2)由(1)可知,當

時,

≤0<1+

,故只需證明

在

時成立,
當

時,

>1,且

,∴

,
設

,

,則

,
當

時,

,當

時,

,
所以當

時,

取得最大值

,
所以

,
綜上,對任意

練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
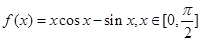
.
(1)求證:

;
(2)若

對

恒成立,求

的最大值與

的最小值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)

(

R),
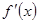
為其導函數(shù),且

時

有極小值

.
(1)求
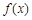
的單調遞減區(qū)間;
(2)若

,

,當

時,對于任意x,

和

的值至少有一個是正數(shù),求實數(shù)m的取值范圍;
(3)若不等式

(

為正整數(shù))對任意正實數(shù)

恒成立,求

的最大值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
求下列函數(shù)的導數(shù):
(1)

;
(2)

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
函數(shù)

(1)

時,求

最小值;
(2)若

在

是單調減函數(shù),求

取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知函數(shù)

(

)的圖象如圖所示,則不等式

的解集為________.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若

,則

等于 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若曲線

處的切線平行于直線

的坐標是_______.
查看答案和解析>>

 為常數(shù),e=2.71828…是自然對數(shù)的底數(shù)),曲線
為常數(shù),e=2.71828…是自然對數(shù)的底數(shù)),曲線 在點
在點 處的切線與x軸平行.
處的切線與x軸平行. 的單調區(qū)間;
的單調區(qū)間; ,其中
,其中 為
為 的導函數(shù).證明:對任意
的導函數(shù).證明:對任意 .
. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 (
( R),
R),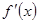 為其導函數(shù),且
為其導函數(shù),且 時
時 有極小值
有極小值 .
.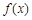 的單調遞減區(qū)間;
的單調遞減區(qū)間; ,
, ,當
,當 時,對于任意x,
時,對于任意x, 和
和 的值至少有一個是正數(shù),求實數(shù)m的取值范圍;
的值至少有一個是正數(shù),求實數(shù)m的取值范圍; (
( 為正整數(shù))對任意正實數(shù)
為正整數(shù))對任意正實數(shù) 恒成立,求
恒成立,求 的最大值.
的最大值.