
分析 (1)由題中條件:“從事蔬菜種植的農民的年總收入不低于動員前從事蔬菜種植的年總收入”得到一個不等關系,列不等式得x的取值范圍;
(2)問題先轉化成一個不等關系,然后轉化為恒成立問題解決.
解答 解:(1)由題意得3(100-x)(1+2x%)≥3×100,
即x2-50x≤0,解得0≤x≤50,
又因為x>0,所以0<x≤50;(6分)
(2)從事蔬菜加工的農民的年總收入為3 (a-$\frac{3}{50}$x)x萬元,從事蔬菜種植農民的年總收入為3(100-x)(1+2x%)萬元,
根據題意得,3 (a-$\frac{3}{50}$x)x≤3(100-x)(1+2x%)恒成立,
又x>0,所以a≤$\frac{100}{x}$+$\frac{x}{25}$+1恒成立,
而$\frac{100}{x}$+$\frac{x}{25}$+1≥5(當且僅當x=50時取得等號),
所以a的最大值為5.(16分)
點評 本題主要考查函數在實際生活中的應用、恒成立問題的解法.求不等式恒成立的參數的取值范圍,是經久不衰的話題,也是高考的熱點,它可以綜合地考查中學數學思想與方法,體現知識的交匯.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:選擇題
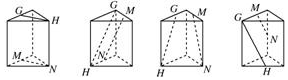
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在一次射擊比賽中,8個泥制的靶子掛成三列,其中兩列各掛3個,一列掛2個,一射手射擊時只準擊碎三列靶子任一列中最下面的一個,若每次射擊都遵循這條原則,則擊碎8個靶子可以有多少種不同的次序?
在一次射擊比賽中,8個泥制的靶子掛成三列,其中兩列各掛3個,一列掛2個,一射手射擊時只準擊碎三列靶子任一列中最下面的一個,若每次射擊都遵循這條原則,則擊碎8個靶子可以有多少種不同的次序?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
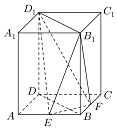 如圖,在正四棱柱ABCD-A1B1C1D1中,底面邊長為2$\sqrt{2}$,側棱長為4,E、F分別
如圖,在正四棱柱ABCD-A1B1C1D1中,底面邊長為2$\sqrt{2}$,側棱長為4,E、F分別查看答案和解析>>
科目:高中數學 來源: 題型:解答題
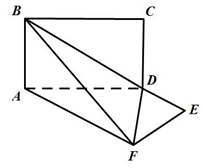 如圖,平面ABCD⊥平面ADEF,其中ABCD為矩形,ADEF為梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.
如圖,平面ABCD⊥平面ADEF,其中ABCD為矩形,ADEF為梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
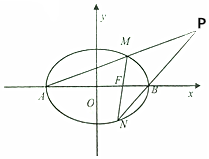 己知橢圓$\frac{x^2}{m}+\frac{y^2}{n}=1$(m>n>0)的離心率e的值為$\frac{1}{2}$,右準線方程為x=4.如圖所示,橢圓C左右頂點分別為A,B,過右焦點F的直線交橢圓C于M,N,直線AM,MB交于點P.
己知橢圓$\frac{x^2}{m}+\frac{y^2}{n}=1$(m>n>0)的離心率e的值為$\frac{1}{2}$,右準線方程為x=4.如圖所示,橢圓C左右頂點分別為A,B,過右焦點F的直線交橢圓C于M,N,直線AM,MB交于點P.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com