
如圖,三角形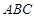 中,
中,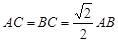 ,
,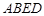 是邊長為
是邊長為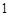 的正方形,平面
的正方形,平面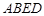 ⊥底面
⊥底面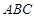 ,若
,若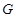 、
、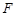 分別是
分別是 、
、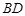 的中點.
的中點.
(1)求證: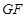 ∥底面
∥底面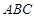 ;
;
(2)求證: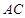 ⊥平面
⊥平面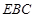 ;
;
(3)求幾何體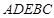 的體積.
的體積.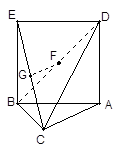
(1)證明過程詳見解析;(2)證明過程詳見解析;(3) .
.
解析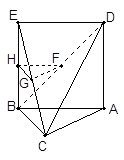
試題分析:本題主要考查線面垂直、線線垂直、面面垂直、線線平行、線面平行、幾何體的體積等基礎知識,考查學生的空間想象能力、邏輯推理能力、轉化能力.第一問,作出輔助線,在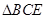 中,HG為中位線,則
中,HG為中位線,則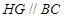 ,在
,在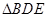 中,HF為中位線,則
中,HF為中位線,則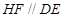 ,
, ,所以
,所以 ,利用線面平行的判定得
,利用線面平行的判定得 平面
平面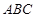 ,
,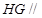 平面
平面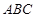 ,再利用面面平行的判定得平面
,再利用面面平行的判定得平面 //平面
//平面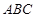 ,利用面面平行的性質得
,利用面面平行的性質得 //平面
//平面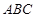 ;第二問,由
;第二問,由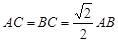 ,得
,得 為直角三角形,
為直角三角形, ,而
,而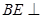 平面
平面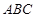 ,則由線面垂直的性質得
,則由線面垂直的性質得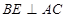 ,由線面垂直的判定得
,由線面垂直的判定得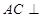 平面
平面 ;第三問,取AB中點,由于
;第三問,取AB中點,由于 為等腰直角三角形,所以
為等腰直角三角形,所以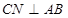 ,而
,而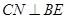 ,所以
,所以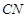 ⊥平面
⊥平面 ,所以CN是錐體的高,利用錐體的體積公式計算體積即可.
,所以CN是錐體的高,利用錐體的體積公式計算體積即可.
(1)取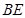 的中點
的中點 ,連結
,連結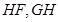 ,
,
因為 分別是
分別是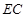 和
和 的中點,所以
的中點,所以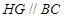 ,
,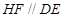 ,
,
又因為 為正方形, 所以
為正方形, 所以 ,從而
,從而 ,
,
所以 平面
平面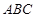 ,
,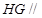 平面
平面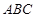 ,
, ,
,
所以平面 //平面
//平面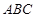 ,所以
,所以 //平面
//平面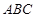 . 4分
. 4分
(2)因為 為正方形,所以
為正方形,所以 ,所以
,所以
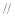 平面
平面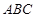 ,
,
又因為平面 ⊥平面
⊥平面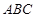 ,所以
,所以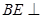 平面
平面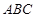 ,
,
所以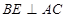 ,又
,又


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:解答題
如圖,四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,點E在線段AD上,且CE∥AB.
(1)求證:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=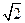 ,∠CDA=45°,求四棱錐P-ABCD的體積.
,∠CDA=45°,求四棱錐P-ABCD的體積.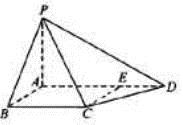
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013•浙江)如圖,在四面體A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2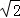 .M是AD的中點,P是BM的中點,點Q在線段AC上,且AQ=3QC.
.M是AD的中點,P是BM的中點,點Q在線段AC上,且AQ=3QC.
(1)證明:PQ∥平面BCD;
(2)若二面角C﹣BM﹣D的大小為60°,求∠BDC的大小.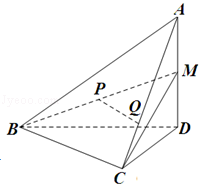
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在如圖所示的幾何體中,四邊形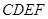 為正方形,四邊形
為正方形,四邊形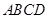 為等腰梯形,
為等腰梯形,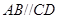 ,
,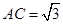 ,
,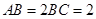 ,
,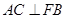 .
.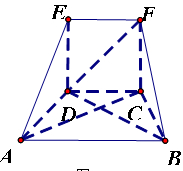
(1)求證: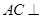 平面
平面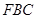 ;
;
(2)求四面體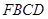 的體積;
的體積;
(3)線段 上是否存在點
上是否存在點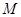 ,使
,使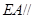 平面
平面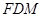 ?請證明你的結論.
?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D為線段BC的中點,E、F為線段AC的三等分點(如圖①).將△ABD沿著AD折起到△AB′D的位置,連結B′C(如圖②).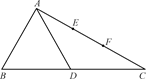
圖①
圖②
(1)若平面AB′D⊥平面ADC,求三棱錐B′-ADC的體積;
(2)記線段B′C的中點為H,平面B′ED與平面HFD的交線為l,求證:HF∥l;
(3)求證:AD⊥B′E.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com