
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У��c(di��n)
�У��c(di��n)![]() �ڙE�A
�ڙE�A![]()
![]() �ϣ��^�c(di��n)
�ϣ��^�c(di��n)![]() ��ֱ��
��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
������E�A![]() ���x���ʣ�
���x���ʣ�
������ֱ��![]() �c
�c![]() �S��
�S��![]() �S�քe�ཻ��
�S�քe�ཻ��![]() ���c(di��n)��ԇ��
���c(di��n)��ԇ��![]() ��e����Сֵ��
��e����Сֵ��
�����O(sh��)�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �c�c(di��n)
�c�c(di��n)![]() �P(gu��n)��ֱ��
�P(gu��n)��ֱ��![]() ��(du��)�Q�����C���c(di��n)
��(du��)�Q�����C���c(di��n)![]() ���c(di��n)������
���c(di��n)������
���𰸡�����![]() ������
������![]() ������Ҋ����
������Ҋ����
��������
������ÙE�AC��a��b��c���\(y��n)���x���ʹ�ʽӋ(j��)�㼴�ɵõ�����ֵ��������ֱ��l�У��քe��x��0��y��0�����A��B������(bi��o)�����������OAB����e����P����E�A���̣��\(y��n)�û�������ʽ���ɵõ�������Сֵ������ӑՓ�ٮ�(d��ng)x0��0�r(sh��)��P��0����1�����ڮ�(d��ng)x0��0�r(sh��)���O(sh��)�c(di��n)Q��m��n�����\(y��n)�Ì�(du��)�Q���քe���Q������(bi��o)���\(y��n)�����c(di��n)�����ėl����б����ȣ����ɵ��C��
�������}���֪![]() ��
��![]() �����ԙE�A
�����ԙE�A![]() �x���ʞ�
�x���ʞ�![]() ��
��
������?y��n)�ֱ��![]() �c
�c![]() �S��
�S��![]() �S�քe�ཻ��
�S�քe�ཻ��![]() ���c(di��n)������
���c(di��n)������![]() ��
��
��![]() ����
����![]() ��
��![]() ���t
���t![]() ��
��
��![]() ����
����![]() ��
��![]() ���t
���t![]() ��
��
����![]() ����e
����e![]() ��
��
��?y��n)��c(di��n)![]() �ڙE�A
�ڙE�A![]()
![]() �ϣ�����
�ϣ�����![]() ��
��
����![]() ����
����![]() ���t
���t![]() ��
��
����![]() ��
��
��(d��ng)�҃H��(d��ng)![]() ����
����![]() �r(sh��)��
�r(sh��)��![]() ��e����Сֵ��
��e����Сֵ��![]() ��
��
���ٮ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����(d��ng)ֱ��
����(d��ng)ֱ��![]() �r(sh��)����
�r(sh��)����![]() ���˕r(sh��)
���˕r(sh��)![]() ��
��![]() ��
��
��?y��n)?/span>![]() ���������c(di��n)
���������c(di��n)![]() ������ͬ������(d��ng)ֱ��
������ͬ������(d��ng)ֱ��![]() �r(sh��)�����c(di��n)
�r(sh��)�����c(di��n)![]() ������
������
�ڮ�(d��ng)![]() �r(sh��)���O(sh��)�c(di��n)
�r(sh��)���O(sh��)�c(di��n)![]() ����?y��n)��c(di��n)
����?y��n)��c(di��n)![]() �c�c(di��n)
�c�c(di��n)![]() �P(gu��n)��ֱ��
�P(gu��n)��ֱ��![]() ��(du��)�Q��
��(du��)�Q��
����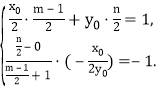 ������
������![]()
���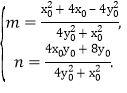 �����c(di��n)
�����c(di��n)![]() ��
��
����?y��n)?/span>![]() ��
��![]() ����
����
![]()
![]()
![]()
![]() ��
��
����![]()
![]() �������c(di��n)
�������c(di��n)![]() ���c(di��n)������
���c(di��n)������
�C���������c(di��n)![]() ���c(di��n)������
���c(di��n)������



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
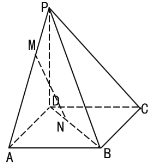
���}Ŀ����D�������FP-ABCD����������Σ�PD��ƽ��ABCD,PD=AD,�c(di��n)M�龀��PA������һ�c(di��n)���������c(di��n)�����c(di��n)N�ھ���BD�ϣ���PM=DN.
��1�����C��ֱ��MN��ƽ��PCD.
��2�����c(di��n)M�龀��PA�����c(di��n)����ֱ��PB�cƽ��AMN���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]() ��(g��)����(sh��)
��(g��)����(sh��)![]() ���·���һ��(g��)�AȦ������
���·���һ��(g��)�AȦ������![]()
![]() �ǹ����
�ǹ����![]() �ĵȲ(sh��)�У���
�ĵȲ(sh��)�У���![]() �ǹ��Ȟ�
�ǹ��Ȟ�![]() �ĵȱȔ�(sh��)��.
�ĵȱȔ�(sh��)��.
��1����![]() ����(sh��)��
����(sh��)��![]() �������(xi��ng)�ĺ�
�������(xi��ng)�ĺ�![]() ��
��
��2����![]() ����
����![]() �����ֵ��
�����ֵ��
��3����(d��ng)![]() �r(sh��)�Ƿ����������(sh��)
�r(sh��)�Ƿ����������(sh��)![]() ���M��
���M��![]() �������ڣ����
�������ڣ����![]() ֵ���������ڣ�Ո�f������.
ֵ���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D1����߅�L��4������![]() �У�
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ����
����![]() ��
��![]() ����
����![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() ����D2��
����D2��

��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
��3���Д��ھ���![]() ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)![]() ��ʹƽ��
��ʹƽ��![]() ƽ��
ƽ��![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ��f�����ɣ�
��ֵ���������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
������![]() �ĈD���cֱ��
�ĈD���cֱ��![]() ���У���
������![]()
������![]() �Һ���(sh��)
�Һ���(sh��)![]() �����c(di��n)��
�����c(di��n)��![]() ,
,
�O(sh��)����(sh��) ԇӑՓ����(sh��)
ԇӑՓ����(sh��)![]() �����c(di��n)��(g��)��(sh��).��
�����c(di��n)��(g��)��(sh��).��![]() ����Ȼ����(sh��)��
����Ȼ����(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �����(xi��ng)
�����(xi��ng)![]() ���O(sh��)ԓ��(sh��)�е�ǰ
���O(sh��)ԓ��(sh��)�е�ǰ![]() �(xi��ng)�ĺ͞�
�(xi��ng)�ĺ͞�![]() ����
����![]()
��1����(sh��)��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2������(sh��)��![]() �M��
�M��![]() ����(sh��)��
����(sh��)��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��3���ڵڣ�2��С�}�ėl���£���![]() ��
��![]() �ǔ�(sh��)��
�ǔ�(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)�ͣ���(du��)
�(xi��ng)�ͣ���(du��)![]() ��
��![]() ���������
���������![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() �dz���(sh��)��
�dz���(sh��)��![]() .
.
��1��������![]() ��
��![]() ̎���о���(j��ng)�^�c(di��n)
̎���о���(j��ng)�^�c(di��n)![]() ����
����![]() ��ֵ��
��ֵ��
��2����![]() ��
��![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��)����ԇ�C�����ٺ���(sh��)
����Ȼ��(du��)��(sh��)�ĵה�(sh��)����ԇ�C�����ٺ���(sh��)![]() �Ѓɂ�(g��)���c(di��n)���ں���(sh��)
�Ѓɂ�(g��)���c(di��n)���ں���(sh��)![]() �ăɂ�(g��)���c(di��n)
�ăɂ�(g��)���c(di��n)![]() �M��
�M��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����![]() ��(g��)��ͬ�ļt���
��(g��)��ͬ�ļt���![]() ��(g��)��ͬ�İ�����ͬһ��(g��)���У��F(xi��n)����ȡ��
��(g��)��ͬ�İ�����ͬһ��(g��)���У��F(xi��n)����ȡ��![]() ��(g��)��.
��(g��)��.
��1����ȡ���ļt��Ă�(g��)��(sh��)�����ڰ���Ă�(g��)��(sh��)���t�ж��ٷN��ͬ��ȡ����
��2��ȡ��һ��(g��)�t��ӛ![]() �֣�ȡ��һ��(g��)����ӛ
�֣�ȡ��һ��(g��)����ӛ![]() �֣���ȡ��
�֣���ȡ��![]() ��(g��)��Ŀ��ֲ�����
��(g��)��Ŀ��ֲ�����![]() �֣��t�ж��ٷN��ͬ��ȡ����
�֣��t�ж��ٷN��ͬ��ȡ����
��3����ȡ����![]() ��(g��)�����һ�����У�ӛ��������������ȡ��
��(g��)�����һ�����У�ӛ��������������ȡ��![]() ��(g��)��Ȼ��Ż������С���һ�β���������������Σ���ǡ��һ��ȡ��
��(g��)��Ȼ��Ż������С���һ�β���������������Σ���ǡ��һ��ȡ��![]() ��(g��)�t����ǡ��һ��ȡ��
��(g��)�t����ǡ��һ��ȡ��![]() ��(g��)����ĸ���.
��(g��)����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����x���A�ĵ�ֱ���ľ��x�c�A�İ돽֮�Ȟ�ֱ���P(gu��n)�ڈA�ľ��x��![]() .
.
��1���O(sh��)�A![]() ���^
���^![]() ��2,0����ֱ���P(gu��n)�ڈA
��2,0����ֱ���P(gu��n)�ڈA![]() �ľ��x��
�ľ��x��![]() ��ֱ�����̣�
��ֱ�����̣�
��2����A![]() �c
�c![]() �S�������c(di��n)
�S�������c(di��n)![]() ��0,3����ֱ��
��0,3����ֱ��![]() =
= ![]() �P(gu��n)�ڈA
�P(gu��n)�ڈA![]() �ľ��x��
�ľ��x��![]() ����ˈA��
����ˈA��![]() �ķ��̣�
�ķ��̣�
��3���Ƿ�����c(di��n)![]() ��ʹ�^
��ʹ�^![]() ������ɗl���ഹֱ��ֱ���քe�P(gu��n)������(y��ng)�ɈA
������ɗl���ഹֱ��ֱ���քe�P(gu��n)������(y��ng)�ɈA![]() �ľ��x��ʼ�K��ȣ������ڣ��������(y��ng)���c(di��n)
�ľ��x��ʼ�K��ȣ������ڣ��������(y��ng)���c(di��n)![]() �c(di��n)����(bi��o)���������ڣ�Ո�f������.
�c(di��n)����(bi��o)���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com