
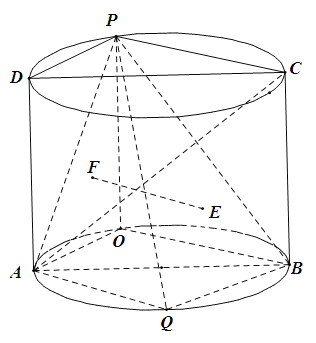
【題目】如圖,圓柱的軸截面![]() 是邊長為2的正方形,點
是邊長為2的正方形,點![]() 是圓弧
是圓弧![]() 上的一動點(不與
上的一動點(不與![]() 重合),點
重合),點![]() 是圓弧
是圓弧![]() 的中點,且點
的中點,且點![]() 在平面
在平面![]() 的兩側.
的兩側.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)設點![]() 在平面
在平面![]() 上的射影為點
上的射影為點![]() ,點
,點![]() 分別是
分別是![]() 和
和![]() 的重心,當三棱錐
的重心,當三棱錐![]() 體積最大時,回答下列問題.
體積最大時,回答下列問題.
(ⅰ)證明:![]() 平面
平面![]() ;
;
(ⅱ)求平面![]() 與平面
與平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)見解析(2)(ⅰ)見解析(ⅱ)![]()
【解析】
(1)證明![]() 垂直平面
垂直平面![]() 內的兩條相交直線
內的兩條相交直線![]() ,再利用面面垂直的判定定理證明即可;
,再利用面面垂直的判定定理證明即可;
(2)當三棱錐![]() 體積最大時,點
體積最大時,點![]() 為圓弧
為圓弧![]() 的中點,所以點
的中點,所以點![]() 為圓弧
為圓弧![]() 的中點,所以四邊形
的中點,所以四邊形![]() 為正方形,且
為正方形,且![]() 平面
平面![]() .(ⅰ)連接
.(ⅰ)連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() ,則
,則![]() ,再由線面平行的判定定理證得結論;(ⅱ)由
,再由線面平行的判定定理證得結論;(ⅱ)由![]() 平面
平面![]() 垂直
垂直![]() ,所以以
,所以以![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸建立空間直角坐標系,求出平面
軸建立空間直角坐標系,求出平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,求兩向量夾角的余弦值,進而得到二面角的正弦值.
,求兩向量夾角的余弦值,進而得到二面角的正弦值.
(1)因為![]() 是軸截面,所以
是軸截面,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又點![]() 是圓弧
是圓弧![]() 上的一動點(不與
上的一動點(不與![]() 重合),且
重合),且![]() 為直徑,所以
為直徑,所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
(2)當三棱錐![]() 體積最大時,點
體積最大時,點![]() 為圓弧
為圓弧![]() 的中點,所以點
的中點,所以點![]() 為圓弧
為圓弧![]() 的中點,所以四邊形
的中點,所以四邊形![]() 為正方形,且
為正方形,且![]() 平面
平面![]() .
.
(ⅰ)連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() ,則
,則![]() ,
,
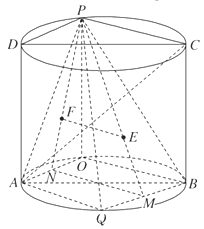
因為![]() 分別為兩個三角形的重心,∴
分別為兩個三角形的重心,∴![]() ,
,![]()
所以![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
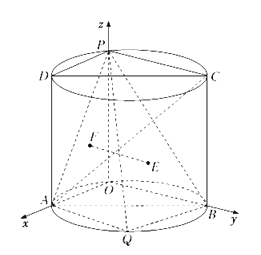
(ⅱ)![]() 平面
平面![]() 垂直
垂直![]() ,所以以
,所以以![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸建立空間直角坐標系,如圖所示:
軸建立空間直角坐標系,如圖所示:
則![]() ,設平面
,設平面![]() 的法向量
的法向量![]() ,則
,則![]() 即
即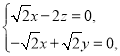 可取
可取![]() ,
,
又平面![]() 的法向量
的法向量![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以平面![]() 與平面
與平面![]() 所成二面角的正弦值為
所成二面角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,已知A,B兩鎮分別位于東西湖岸MN的A處和湖中小島的B處,點C在A的正西方向1 km處,tan∠BAN=![]() ,∠BCN=
,∠BCN=![]() ,.現計劃鋪設一條電纜連通A,B兩鎮,有兩種鋪設方案:①沿線段AB在水下鋪設;②在湖岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設,預算地下、水下的電纜鋪設費用分別為2萬元km、4萬元km.
,.現計劃鋪設一條電纜連通A,B兩鎮,有兩種鋪設方案:①沿線段AB在水下鋪設;②在湖岸MN上選一點P,先沿線段AP在地下鋪設,再沿線段PB在水下鋪設,預算地下、水下的電纜鋪設費用分別為2萬元km、4萬元km.
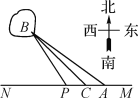
(1)求A,B兩鎮間的距離;
(2)應該如何鋪設,使總鋪設費用最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在坐標原點焦點在x軸上,橢圓C上一點A(2![]() ,﹣1)到兩焦點距離之和為8.若點B是橢圓C的上頂點,點P,Q是橢圓C上異于點B的任意兩點.
,﹣1)到兩焦點距離之和為8.若點B是橢圓C的上頂點,點P,Q是橢圓C上異于點B的任意兩點.
(1)求橢圓C的方程;
(2)若BP⊥BQ,且滿足3![]() 2
2![]() 的點D在y軸上,求直線BP的方程;
的點D在y軸上,求直線BP的方程;
(3)若直線BP與BQ的斜率乘積為常數λ(λ<0),試判斷直線PQ是否經過定點.若經過定點,請求出定點坐標;若不經過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為
的長軸長為![]() ,焦距為2,拋物線
,焦距為2,拋物線![]() 的準線經過橢圓
的準線經過橢圓![]() 的左焦點
的左焦點![]() .
.
(1)求橢圓![]() 與拋物線
與拋物線![]() 的方程;
的方程;
(2)直線![]() 經過橢圓
經過橢圓![]() 的上頂點且
的上頂點且![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() ,
,![]() 與拋物線
與拋物線![]() 分別交于點
分別交于點![]() (異于點
(異于點![]() ),
),![]() (異于點
(異于點![]() ),證明:直線
),證明:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究不同性別在處理多任務時的表現差異,召集了男女志愿者各200名,要求他們同時完成多個任務,包括解題、讀地圖、接電話.下圖表示了志愿者完成任務所需的時間分布.以下結論,對志愿者完成任務所需的時間分布圖表理解正確的是( )

①總體看女性處理多任務平均用時更短;
②所有女性處理多任務的能力都要優于男性;
③男性的時間分布更接近正態分布;
④女性處理多任務的用時為正數,男性處理多任務的用時為負數.
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某縣一中學的同學為了解本縣成年人的交通安全意識情況,利用假期進行了一次全縣成年人安全知識抽樣調查.已知該縣成年人中![]() 的擁有駕駛證,先根據是否擁有駕駛證,用分層抽樣的方法抽取了100名成年人,然后對這100人進行問卷調查,所得分數的頻率分布直方圖如下圖所示.規定分數在80以上(含80)的為“安全意識優秀”.
的擁有駕駛證,先根據是否擁有駕駛證,用分層抽樣的方法抽取了100名成年人,然后對這100人進行問卷調查,所得分數的頻率分布直方圖如下圖所示.規定分數在80以上(含80)的為“安全意識優秀”.
擁有駕駛證 | 沒有駕駛證 | 合計 | |
得分優秀 | |||
得分不優秀 | 25 | ||
合計 | 100 |

(1)補全上面![]() 的列聯表,并判斷能否有超過
的列聯表,并判斷能否有超過![]() 的把握認為“安全意識優秀與是否擁有駕駛證”有關?
的把握認為“安全意識優秀與是否擁有駕駛證”有關?
(2)若規定參加調查的100人中分數在70以上(含70)的為“安全意識優良”,從參加調查的100人中根據安全意識是否優良,按分層抽樣的方法抽出5人,再從5人中隨機抽取3人,試求抽取的3人中恰有一人為“安全意識優良”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線l過點
的直線l過點![]() ,以原點
,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的參數方程(
的參數方程(![]() 為常數)和曲線
為常數)和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求傾斜角
,求傾斜角![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com