
【題目】已知函數f(x)=loga ![]() ,g(x)=1+loga(x﹣1),(a>0且a≠1),設f(x)和g(x)的定義域的公共部分為D,
,g(x)=1+loga(x﹣1),(a>0且a≠1),設f(x)和g(x)的定義域的公共部分為D,
(1)求集合D;
(2)當a>1時.若不等式g(x﹣ ![]() )﹣f(2x)>2在D內恒成立,求a的取值范圍;
)﹣f(2x)>2在D內恒成立,求a的取值范圍;
(3)是否存在實數a,當[m,n]D時,f(x)在[m,n]上的值域是[g(n),g(m)],若存在,求實數a的取值范圍,若不存在說明理由.
【答案】
(1)解:f(x)的定義域為:
![]() >0,
>0,
∴x>3或x<﹣3;
g(x)的定義域為:
x﹣1>0,
∴x>1,
∴集合D為(3,+∞)
(2)解:1+loga(x﹣ ![]() )﹣loga
)﹣loga ![]() >2,
>2,
∴loga ![]() >1,
>1,
∴a< ![]() ,
,
設h(x)= ![]() ,t=2x﹣3,
,t=2x﹣3,
∴g(t)= ![]() =
= ![]() (t+
(t+ ![]() )+
)+ ![]() ,
,
∴g(t)>g(3)= ![]() ,
,
∴1<a≤ ![]()
(3)解:f(x)=loga(1﹣ ![]() ),μ(t)=1﹣
),μ(t)=1﹣ ![]() 在(3,+∞)上遞增,μ(3)=0,
在(3,+∞)上遞增,μ(3)=0,
當a>1時,f(x)在3,+∞)上遞增,g(x)在3,+∞)上遞增,
當m<n時,g(m)<g(n),不合題意,舍去;
當0<a<1時,f(x)在3,+∞)上遞減,g(x)在3,+∞)上遞減,
由f(m)=g(m),f(n)=g(n),
∴m,n是f(x)=g(x)的兩根,
∴ ![]() =a(x﹣1),
=a(x﹣1),
∴ax2+(2a﹣1)x﹣3a+3=0,
∴m+n>6,mn>9,
∴a< ![]() ,
,
又m+n>2 ![]() ,
,
∴a< ![]() 或a>
或a> ![]() ,
,
又△>0,(2a﹣1)2﹣4a(3﹣3a)>0
∴a< ![]() 或a>
或a> ![]() ,
,
∴0<a< ![]()
【解析】(1)利用對數函數的定義求定義域即可;(2)整理不等式得a< ![]() ,構造函數g(t)=
,構造函數g(t)= ![]() =
= ![]() (t+
(t+ ![]() )+
)+ ![]() ,求出g(t)的最小值;(3)對參數a進行分類討論,當a>1時,f(x)在3,+∞)上遞增,g(x)在3,+∞)上遞增,不合題意,舍去;
,求出g(t)的最小值;(3)對參數a進行分類討論,當a>1時,f(x)在3,+∞)上遞增,g(x)在3,+∞)上遞增,不合題意,舍去;
當0《a<1時,f(x)在3,+∞)上遞減,g(x)在3,+∞)上遞減,構造m,n是f(x)=g(x)的兩根,利用二次方程有解求出a的范圍.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數學 來源: 題型:
【題目】對于函數f(x)定義域中任意的x1 , x2(x1≠x2)有如下結論
1)f(x1+x2)=f(x1)f(x2)
2)f(x1x2)=f(x1)+f(x2)
3) ![]() >0
>0
4)f( ![]() )<
)< ![]()
5)f( ![]() )>
)> ![]()
6)f(﹣x)=f(x).
當f(x)=lgx時,上述結論正確的序號為 . (注:把你認為正確的命題的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列三個命題:
①若一個球的半徑縮小到原來的 ![]() ,則其體積縮小到原來的
,則其體積縮小到原來的![]() ;
;
②若兩組數據的平均數相等,則它們的標準差也相等;
③直線x+y+1=0與圓x2+y2= ![]() 相切.
相切.
其中真命題的序號是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間生產某種產品,固定成本是![]() 萬元,每生產
萬元,每生產![]() 件產品成本增加
件產品成本增加![]() 元,根據經驗,當年產量少于400件時,總收益
元,根據經驗,當年產量少于400件時,總收益![]() (成本與總利潤的和,單位:元)是年產量
(成本與總利潤的和,單位:元)是年產量![]() (單位:件)的二次函數;,當年產量不少于
(單位:件)的二次函數;,當年產量不少于![]() 件時,R是Q的一次函數,以下是Q與R的部分數據:
件時,R是Q的一次函數,以下是Q與R的部分數據:
Q/ 件 | 50 | 200 | 350 | 500 | 650 |
R/ 元 | 23750 | 80000 | 113750 | 125000 | 1332500 |
問:每年生產多少件產品時,總利潤最大?最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lg(x2+ax﹣a﹣1),給出下述命題:
①f(x)有最小值;
②當a=0時,f(x)的值域為R;
③若f(x)在區間[2,+∞)上單調遞增,則實數a的取值范圍是a≥﹣4;
④a=1時,f(x)的定義域為(﹣1,0);
則其中正確的命題的序號是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知指數函數y=g(x)滿足:g(3)=8,定義域為R的函數f(x)= ![]() 是奇函數.
是奇函數.
(1)確定y=f(x)和y=g(x)的解析式;
(2)若對任意的x∈[1,4],不等式f(2x﹣3)+f(x﹣k)>0恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為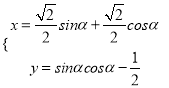 (
(![]() 為參數),若以直角坐標系中的原點為極點,
為參數),若以直角坐標系中的原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() 為實數.)
為實數.)
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 與曲線
與曲線![]() 有公共點,求
有公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為考察高中生的性別與是否喜歡數學課程之間的關系,在我市某普通中學高中生中隨機抽取200名學生,得到如下2×2列聯表:
喜歡數學課 | 不喜歡數學課 | 合計 | |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合計 | 50 | 150 | 200 |
經計算K2≈6.06,根據獨立性檢驗的基本思想,約有(填百分數)的把握認為“性別與喜歡數學課之間有關系”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com