
 ,|x-2|},其中min{a,b}=
,|x-2|},其中min{a,b}=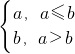 ,若動直線y=m與函數y=f(x)f(x)的圖象有三個不同的交點,它們的橫坐標分別為x1,x2,x3,則x1•x2•x3是否存在最大值?若存在,在橫線處填寫其最大值;若不存在,直接填寫“不存在”________.
,若動直線y=m與函數y=f(x)f(x)的圖象有三個不同的交點,它們的橫坐標分別為x1,x2,x3,則x1•x2•x3是否存在最大值?若存在,在橫線處填寫其最大值;若不存在,直接填寫“不存在”________.
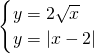 解得A(4-2
解得A(4-2 ,2
,2 -2),
-2), -2.
-2. =m得x1=
=m得x1=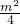 ,由|x2-2|=2-x2=m,得x2=2-m,由|x3-2|=x3-2=m,得x3=m+2,
,由|x2-2|=2-x2=m,得x2=2-m,由|x3-2|=x3-2=m,得x3=m+2,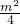 ×(2-m)×(2+m)=
×(2-m)×(2+m)= •m2•(4-m2)≤
•m2•(4-m2)≤ •
•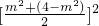 =1,
=1, 時取得等號,
時取得等號,

 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:高中數學 來源: 題型:
| x |
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com