
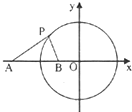
 已知圓C:x2+y2=9,點A(-5,0),直線l:x-2y=0.
已知圓C:x2+y2=9,點A(-5,0),直線l:x-2y=0.分析 (1)先求與直線l垂直的直線的斜率,可得其方程,利用相切求出結果.
(2)先設存在,利用都有$\frac{|PB|}{|PA|}$為一常數這一條件,以及P在圓上,列出關系,利用恒成立,可以求得結果.
解答 解:(1)設所求直線方程為y=-2x+b,即2x+y-b=0.
∵直線與圓相切,∴$\frac{{|{-b}|}}{{\sqrt{{2^2}+{1^2}}}}=3$,…(2分)
得$b=±3\sqrt{5}$,…(3分)
∴所求直線方程為$y=-2x±3\sqrt{5}$. …(4分)
(2)方法1:假設存在這樣的點B(t,0).
當P為圓C與x軸的左交點(-3,0)時,$\frac{{|{PB}|}}{{|{PA}|}}=\frac{{|{t+3}|}}{2}$;
當P為圓C與x軸的右交點(3,0)時,$\frac{{|{PB}|}}{{|{PA}|}}=\frac{{|{t-3}|}}{8}$. …(6分)
依題意,$\frac{{|{t+3}|}}{2}=\frac{{|{t-3}|}}{8}$,解得,t=-5(舍去),或$t=-\frac{9}{5}$. …(8分)[
下面證明當點B的坐標為$(-\frac{9}{5},0)$時,對于圓C上任一點P,$\frac{{|{PB}|}}{{|{PA}|}}$恒為一常數:
設P(x,y),則y2=9-x2,
∴$\frac{{{{|{PB}|}^2}}}{{{{|{PA}|}^2}}}=\frac{{{{(x+\frac{9}{5})}^2}+{y^2}}}{{{{(x+5)}^2}+{y^2}}}=\frac{{\frac{18}{25}(5x+17)}}{2(5x+17)}=\frac{9}{25}$,
從而$\frac{{|{PB}|}}{{|{PA}|}}=\frac{3}{5}$為常數. …(12分)
方法2:假設存在這樣的點B(t,0),使得$\frac{{|{PB}|}}{{|{PA}|}}$為常數λ,則PB2=λ2PA2,
∴(x-t)2+y2=λ2[(x+5)2+y2],
將y2=9-x2代入得x2-2tx+t2+9-x2=λ2(x2+10x+25+9-x2),…(6分)
即2(5λ2+t)x+34λ2-t2-9=0對x∈[-3,3]恒成立,…(8分)
∴$\left\{{\begin{array}{l}{5{λ^2}+t=0}\\{34{λ^2}-{t^2}-9=0}\end{array}}\right.$,…(10分)
解得$\left\{{\begin{array}{l}{λ=\frac{3}{5}}\\{t=-\frac{9}{5}}\end{array}}\right.或\left\{{\begin{array}{l}{λ=1}\\{t=-5}\end{array}}\right.(舍去)$,…(11分)
所以存在點$B(-\frac{9}{5},0)$對于圓C上任一點P,都有$\frac{{|{PB}|}}{{|{PA}|}}$為常數$\frac{3}{5}$. …(12分)
點評 本題考查直線和圓的方程的應用,圓的切線方程,又是存在性和探究性問題,恒成立問題,考查計算能力.是難題.


 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {a|a<-1} | B. | {a|a≥2} | C. | {a|-1<a<2} | D. | {a|a≤-1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -540 | B. | -270 | C. | 540 | D. | 270 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∨q | B. | p∧q | C. | (¬p)∨(¬q) | D. | (¬p)∨q |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com