
【題目】三位數中,如果百位數字、十位數字、個位數字剛好能構成等差數列,則稱為“等差三位數”,例如:147,642,777,420等等.等差三位數的總個數為( )
A.32B.36C.40D.45
【答案】D
【解析】
由題意分公差為0,1,2,3,4,-1,-2,-3,-4九種情況,分別得出各三位數的個數,運用加法原理可得選項.
由題意得若百位數字、十位數字、個位數字構成公差為0的“等差三位數”,則只要各位數字不為零即可,有9個;
若百位數字、十位數字個位數字構成公差為1的“等差三位數”,則百位數字不大于7,有7個;
若百位數字、十位數字、個位數字構成公差為2的“等差三位數”,則百位數字不大于5,有5個;
若百位數字十位數字個位數字構成公差為3的“等差三位數”,則百位數字不大于3,有3個;若百位數字、十位數字、個位數字構成公差為4的“等差三位數”,則百位數字只能為1,有1個;
若百位數字、十位數字、個位數字構成公差為![]() 的“等差三位數,則百位數字不小于2,有8個;
的“等差三位數,則百位數字不小于2,有8個;
若百位數字、十位數字、個位數字構成公差為![]() 的“等差三位數”,則百位數字不小于4,有6個;
的“等差三位數”,則百位數字不小于4,有6個;
若百位數字、十位數字、個位數字構成公差為![]() 的“等差三位數”,則百位數字不小于6,有4個;
的“等差三位數”,則百位數字不小于6,有4個;
若百位數字、十位數字個位數字構成公差為![]() 的“等差三位數”,則百位數字不小于8有2個.
的“等差三位數”,則百位數字不小于8有2個.
綜上所述,“等差三位數”的總數為![]() 個,
個,
故選:D.


科目:高中數學 來源: 題型:
【題目】設F是橢圓![]() 的左焦點,過點F且斜率為正的直線與E相交于A、B兩點,過點A、B分別作直線AM和BN滿足AM⊥l,BN⊥l,且直線AM、BN分別與x軸相交于M和N.試求|MN|的最小值.
的左焦點,過點F且斜率為正的直線與E相交于A、B兩點,過點A、B分別作直線AM和BN滿足AM⊥l,BN⊥l,且直線AM、BN分別與x軸相交于M和N.試求|MN|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,曲線
為參數),以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,設曲線
,設曲線![]() 與曲線
與曲線![]() 的公共弦所在直線為l.
的公共弦所在直線為l.
(1)在直角坐標系下,求曲線![]() 與曲線
與曲線![]() 的普通方程;
的普通方程;
(2)若以坐標原點為中心,直線l順時針方向旋轉![]() 后與曲線
后與曲線![]() 、曲線
、曲線![]() 分別在第一象限交于A、B兩點,求
分別在第一象限交于A、B兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
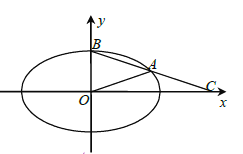
【題目】如圖所示,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,
,![]() 為橢圓
為橢圓![]() 上位于第一象限上的點,
上位于第一象限上的點,![]() 為橢圓
為橢圓![]() 的上頂點,直線
的上頂點,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,
,![]() ,
,![]() 的面積為6.
的面積為6.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若直線![]() 與橢圓
與橢圓![]() 有且只有一個公共點,設橢圓
有且只有一個公共點,設橢圓![]() 的兩焦點到直線
的兩焦點到直線![]() 的距離分別是
的距離分別是![]() ,
,![]() ,試問
,試問![]() 是否為定值?若是,求出其值;若不是,說明理由.
是否為定值?若是,求出其值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓C:![]() 的離心率為
的離心率為![]() ,其右焦點到橢圓C外一點
,其右焦點到橢圓C外一點![]() 的距離為
的距離為![]() ,不過原點O的直線l與橢圓C相交于A,B兩點,且線段AB的長度為2.
,不過原點O的直線l與橢圓C相交于A,B兩點,且線段AB的長度為2.
![]() 1
1![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 2
2![]() 求
求![]() 面積S的最大值.
面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1(﹣c,0),F2(c,0)分別為雙曲線![]() 1(a>0,b>0)的左、右焦點,以坐標原點O為圓心,c為半徑的圓與雙曲線在第二象限交于點P,若tan∠PF1F2
1(a>0,b>0)的左、右焦點,以坐標原點O為圓心,c為半徑的圓與雙曲線在第二象限交于點P,若tan∠PF1F2![]() ,則該雙曲線的離心率為_____.
,則該雙曲線的離心率為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南北朝時期的數學家祖暅提出了計算幾何體體積的祖暅原理:“冪勢既同,則積不容異“.意思是兩個同高的幾何體,如果在等高處的截面積都相等,那么這兩個幾何體的體積相等.現有某幾何體和一個圓錐滿足祖暅原理的條件,若該圓錐的側面展開圖是半徑為3的圓的三分之一,則該幾何體的體積為( )
A.![]() πB.
πB.![]() πC.4
πC.4![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】基于移動互聯技術的共享單車被稱為“新四大發明”之一,短時間內就風靡全國,帶給人們新的出行體驗,某共享單車運營公司的市場研究人員為了解公司的經營狀況,對該公司最近六個月內的市場占有率進行了統計,設月份代碼為x,市場占有率為y(%),得結果如下表
年月 | 2019.11 | 2019.12 | 2020.1 | 2020.2 | 2020.3 | 2020.4 |
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 9 | 11 | 14 | 13 | 18 | 19 |
(1)觀察數據,可用線性回歸模型擬合y與x的關系,請用相關系數加以說明(精確到0.001);
(2)求y關于x的線性回歸方程,并預測該公司2020年6月份的市場占有率;
(3)根據調研數據,公司決定再采購一批單車投入市場,現有采購成本分別為1000元/輛和800元/輛的甲、乙兩款車型,報廢年限不相同.考慮到公司的經濟效益,該公司決定先對這兩款單車各100輛進行科學模擬測試,得到兩款單車使用壽命統計如下表:
車輛數 車型 | 1年 | 2年 | 3年 | 4年 | 總計 |
甲款 | 10 | 40 | 30 | 20 | 100 |
乙款 | 15 | 35 | 40 | 10 | 100 |
經測算,平均每輛單車每年可以為公司帶來收入500元,不考慮除采購成本之外的其他成本,假設每輛單車的使用壽命都是整數年,且用頻率估計每輛單車使用壽命的概率,以每輛單車產生利潤的期望值為決策依據,如果你是該公司的負責人,你會選擇采購哪款車型?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式,相關系數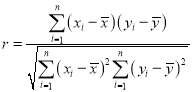 ,回歸方程
,回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為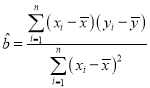 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com