
橢圓E的中心在原點O,焦點在x軸上,離心率e=![]() ,過點C(-1,0)的直線l交橢圓于A、B兩點,且滿足
,過點C(-1,0)的直線l交橢圓于A、B兩點,且滿足![]() =λ
=λ![]() (λ≥2).
(λ≥2).
(1)若λ為常數,試用直線l的斜率k(k≠0)表示△OAB的面積;
(2)若λ為常數,當△OAB的面積取得最大值時,求橢圓E的方程;
(3)若λ變化,且λ=k2+1,試問:實數λ和直線l的斜率k(k∈R)分別為何值時,橢圓E的短半軸取得最大值?并求此時的橢圓方程.
|
解:設橢圓方程為 由 e=故橢圓方程為 x2+3y2=3b2. ①(1)因為直線l:y=k(x+1)交橢圓于A(x1,y1),B(x2,y2)兩點,并且 ∴ (x1+1,y1)=λ(-1-x2,-y2).即 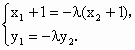 ② ②
把 y=k(x+1)代入橢圓得(3k2+1)x2+6k2x+3k2-3b2=0, 且Δ= k2(3b2-1)+b2>0,∴ x1+x2=-x1x2= 因此 S△OAB=聯立②、③得 x2+1=∴ S△OAB=(2)S= 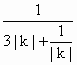 ≤ ≤當且僅當 3|k|=又 x1+1=-λ(x2+1),∴x1=將 x1,x2代入④得3b2=故橢圓方程 x2+3y2=(3)由②、③聯立得x1= 將 x1,x2代入④得3b2=由 k2=λ-1得3b2=易知,當λ≥ 2時,3b2是λ的減函數,故當λ=2時,(3b2)max=3.所以,當λ= 2,k=±1時,橢圓短半軸的長取得最大值,此時橢圓方程為x2+3y2=3.分析:首先考查橢圓的性質.在 (1)中既考查了直線方程、向量和二次方程等知識,又體現了轉化思想的應用;在(2)中,考查了利用不等式求最值;在(3)中,既要運用數形結合思想和轉化思想,巧妙地把與橢圓有關的最值問題轉化為函數的最值問題,又要利用函數的單調性求最值. |
|
評注:本題以直線與橢圓為背景,向量為“紐帶”,把方程、不等式、函數聯系起來,體現了在方程,不等式、函數等知識網絡交匯處命題的思想. |


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
|
| CA |
| BC |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年黑龍江省雞西市高三上學期期末理科數學卷 題型:解答題
橢圓E的中心在原點O,焦點在x軸上,離心率e= ,過點C(-1,0)的直線
,過點C(-1,0)的直線 交橢圓于A,B兩點,且滿足
交橢圓于A,B兩點,且滿足 ,
, 為常數。
為常數。
(1)當直線 的斜率k=1且
的斜率k=1且 時,求三角形OAB的面積.
時,求三角形OAB的面積.
(2)當三角形OAB的面積取得最大值時,求橢圓E的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分)橢圓E的中心在原點O,焦點在x軸上,離心率e=![]() ,過點C(-1,0)的直線
,過點C(-1,0)的直線![]() 交橢圓于A,B兩點,且滿足
交橢圓于A,B兩點,且滿足![]() ,
,![]() 為常數。
為常數。
(1)當直線![]() 的斜率k=1且
的斜率k=1且![]() 時,求三角形OAB的面積.
時,求三角形OAB的面積.
(2)當三角形OAB的面積取得最大值時,求橢圓E的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
橢圓E的中心在原點O,焦點在![]() 軸上,其離心率
軸上,其離心率![]() , 過點C(-1,0)的直線
, 過點C(-1,0)的直線![]() 與橢圓E相交于A、B兩點,且滿足點C分向量
與橢圓E相交于A、B兩點,且滿足點C分向量![]() 的比為2.
的比為2.
(1)用直線![]() 的斜率k ( k≠0 ) 表示△OAB的面積;(2)當△OAB的面積最大時,求橢圓E的方程。
的斜率k ( k≠0 ) 表示△OAB的面積;(2)當△OAB的面積最大時,求橢圓E的方程。
查看答案和解析>>
科目:高中數學 來源:2010年河南省鄭州47中高考模擬數學試卷(解析版) 題型:解答題
 ,過點C(-1,0)的直線l交橢圓于A、B兩點,且滿足:
,過點C(-1,0)的直線l交橢圓于A、B兩點,且滿足: (λ≥2).
(λ≥2).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com