Question

10．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}+6x+3，（x≤0）}\\{-3x+3，（0＜x＜1）}\\{-{x}^{2}+4x-3，（x≥1）}\end{array}\right.$
（1）畫出函數的圖象 （2）根據圖象寫出f（x）單調區間
（3）利用單調性定義證明f（x）在（-∞，-3]上減少的．

Answer 1

分析 （1）由f（x）解析式，利用分段函數能畫出函數的圖象．
（2）根據圖象得到f（x）單調增區間和單調減區間．
（3）x∈（-∞，-3]，f（x）=-x²+4x-3，在（-∞，-3]上任取x₁，x₂，令x₁＜x₂，由此利用定義法能證明f（x）在（-∞，-3]上單調遞減．

解答 解：（1）∵f（x）=$\left\{\begin{array}{l}{{x}^{2}+6x+3，（x≤0）}\\{-3x+3，（0＜x＜1）}\\{-{x}^{2}+4x-3，（x≥1）}\end{array}\right.$，
∴畫出函數的圖象，如下圖：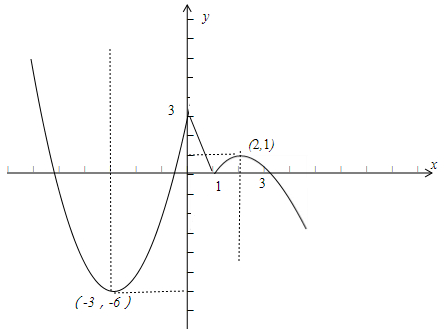

（2）根據圖象得到f（x）單調增區間為（（-3，0），（1，2），
單調減區間是（-∞，3），（0，1），（2，+∞）．
證明：（3）∵x∈（-∞，-3]，∴f（x）=-x²+4x-3，
在（-∞，-3]上任取x₁，x₂，令x₁＜x₂，
則f（x₁）-f（x₂）=（-${{x}_{1}}^{2}+4{{x}_{1}-3}^{\;}$）-（$-{{x}_{2}}^{2}+4{x}_{2}-3$）=（x₂+x₁）（x₂-x₁）+4（x₁-x₂）=（x₂-x₁）（x₁+x₂-4），
∵x₁，x₂∈（-∞，-3]，x₁＜x₂，
∴x₂-x₁＞0，x₁+x₂-4＜0，
∴f（x₁）-f（x₂）＜0，
∴f（x）在（-∞，-3]上單調遞減．

點評 本題考查分段函數的作法，考查函數的單調區間的求法，考查函數的單調性質的證明，是基礎題，解題時要認真審題，注意函數性質的合理運用．