
由函數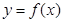 確定數列
確定數列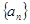 ,
,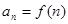 .若函數
.若函數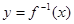 能確定數列
能確定數列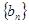 ,
,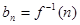 ,則稱數列
,則稱數列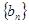 是數列
是數列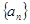 的“反數列”.
的“反數列”.
(1)若函數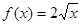 確定數列
確定數列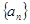 的反數列為
的反數列為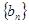 ,求
,求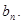 ;
;
(2)對(1)中的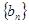 ,不等式
,不等式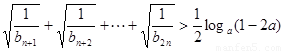 對任意的正整數
對任意的正整數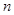 恒成立,求實數
恒成立,求實數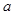 的取值范圍;
的取值范圍;
(3)設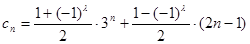 (
(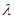 為正整數),若數列
為正整數),若數列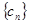 的反數列為
的反數列為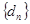 ,
,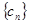 與
與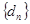 的公共項組成的數列為
的公共項組成的數列為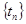 (公共項
(公共項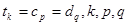 為正整數),求數列
為正整數),求數列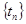 的前
的前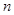 項和
項和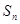 .
.
(1)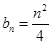 ;(2)
;(2)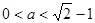 ;(3)
;(3)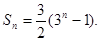
【解析】
試題分析:(1)本題實質是求函數 的反函數
的反函數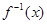 ;(2)不等式恒成立,因此
;(2)不等式恒成立,因此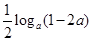 小于不等式左邊的最小值,所以我們一般想辦法求左邊
小于不等式左邊的最小值,所以我們一般想辦法求左邊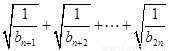 這個和,然而由(1)知
這個和,然而由(1)知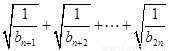
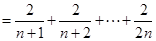 ,這個和求不出,那么我們只能從另一角度去思考,看
,這個和求不出,那么我們只能從另一角度去思考,看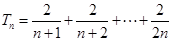 的單調性,這里只要作差
的單調性,這里只要作差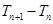 就可得出
就可得出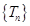 是遞增數列,所以
是遞增數列,所以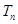 的最小值是
的最小值是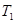 ,問題解決;(3)看起來
,問題解決;(3)看起來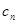 很復雜,實質上由于
很復雜,實質上由于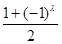 和
和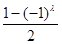 取值只能是0和1,因此我們按
取值只能是0和1,因此我們按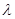 的奇偶性分類討論,問題就簡化了,例如當
的奇偶性分類討論,問題就簡化了,例如當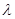 為奇數時,
為奇數時,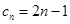 ,則
,則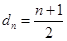 ,就可求出
,就可求出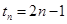 ,從而求出
,從而求出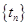 的前
的前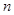 項和了.
項和了.
試題解析:(1)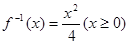 ,則
,則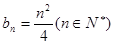 ;4分
;4分
(2)不等式化為: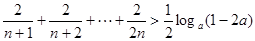 ,5分
,5分
設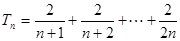 ,因為
,因為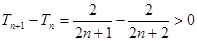 ,
,
所以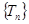 單調遞增,
7分
單調遞增,
7分
則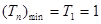 .因此
.因此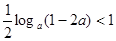 ,即
,即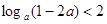 .因為
.因為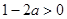 ,
,
所以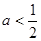 ,
,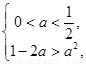 得
得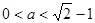 .
10分
.
10分
(3)當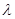 為奇數時,
為奇數時,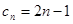 ,
,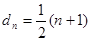 .
11分
.
11分
由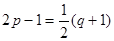 ,則
,則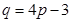 ,
,
即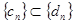 ,因此
,因此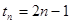 ,
13分
,
13分
所以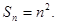 14分
14分
當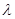 為偶數時,
為偶數時,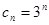 ,
,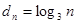 .
15分
.
15分
由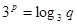 得
得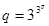 ,即
,即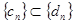 ,因此
,因此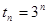 , 17分
, 17分
所以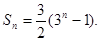 18分
18分
考點:(1)反函數;(2)數列的單調性;(3)分類討論,等差數列與等比數列的前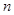 項和.
項和.


科目:高中數學 來源: 題型:
(09年長郡中學一模文)(13分)
由函數![]() 確定數列
確定數列![]() ,
,![]() ,函數
,函數![]() 的反函數
的反函數![]() 能確定數列
能確定數列![]() ,
,![]() ,若對于任意
,若對于任意![]() 都有
都有![]() ,則稱數列
,則稱數列![]() 是數列
是數列![]() 的“自反函數列”.
的“自反函數列”.
(I)設函數![]() ,若由函數
,若由函數![]() 確定的數列
確定的數列![]() 的自反數列為
的自反數列為![]() ,求
,求![]() ;
;
(Ⅱ)已知正數數列![]() 的前n項和
的前n項和 ,寫出
,寫出![]() 表達式,并證明你的結論;
表達式,并證明你的結論;
(Ⅲ)在(I)和(Ⅱ)的條件下,![]() ,當
,當![]() 時,設
時,設![]() ,
,![]() 是數列
是數列![]() 的前
的前![]() 項和,且
項和,且![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年莆田四中一模理) (14分)
由函數![]() 確定數列
確定數列![]() ,
,![]() ,若函數
,若函數![]() 的反函數
的反函數![]() 能確定數列
能確定數列![]() ,
,![]() ,則稱數列
,則稱數列![]() 是數列
是數列![]() 的“反數列”。
的“反數列”。
(1)若函數![]() 確定數列
確定數列![]() 的反數列為
的反數列為![]() ,求
,求![]() 的通項公式;
的通項公式;
(2)對(1)中![]() ,不等式
,不等式![]() 對任意的正整數
對任意的正整數![]() 恒成立,求實數
恒成立,求實數![]() 的范圍;
的范圍;
(3)設![]() ,若數列
,若數列![]() 的反數列為
的反數列為![]() ,
,![]() 與
與![]() 的公共項組成的數列為
的公共項組成的數列為![]() ;求數列
;求數列![]() 前
前![]() 項和
項和![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年惠州一中模擬理) 由函數![]() 確定數列
確定數列![]() ,
,![]() ,若函數
,若函數![]() 的反函數
的反函數![]() 能確定數列
能確定數列![]() ,
,![]() ,則稱數列
,則稱數列![]() 是數列
是數列![]() 的“反數列”。
的“反數列”。
(1)已知函數![]() 的反函數為
的反函數為![]() ,則由函數
,則由函數![]() 確定的數列
確定的數列![]() 的反數列為
的反數列為![]() ,求
,求![]() 的通項公式;不等式
的通項公式;不等式![]() 對任意的正整數
對任意的正整數![]() 恒成立,求實數
恒成立,求實數![]() 的范圍;
的范圍;
(2)設函數![]() 確定的數列為
確定的數列為![]() ,
,![]() 的反數列為
的反數列為![]() ,
,![]() 與
與![]() 的公共項組成的數列為
的公共項組成的數列為![]() ;求數列
;求數列![]() 前
前![]() 項和
項和![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)
由函數![]() 確定數列
確定數列![]() ,
,![]() ,若函數
,若函數![]() 的反函數
的反函數![]() 能確定數列
能確定數列![]() ,
,![]() ,則稱數列
,則稱數列![]() 是數列
是數列![]() 的“反數列”。
的“反數列”。
(1)若函數![]() 確定數列
確定數列![]() 的反數列為
的反數列為![]() ,求
,求![]() 的通項公式;
的通項公式;
(2)對(1)中![]() ,不等式
,不等式![]() 對任意的正整數
對任意的正整數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若數列
,若數列![]() 的反數列為
的反數列為![]() ,
,![]() 與
與![]() 的公共項組成的數列為
的公共項組成的數列為![]() , 求數列
, 求數列![]() 前
前![]() 項和
項和![]() 。
。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com