【題目】如圖，雙曲線
的兩頂點為
，
，虛軸兩端點為
，
，兩焦點為
，
，若以
為直徑的圓內切于菱形
，切點分別為
，
，
，
.則
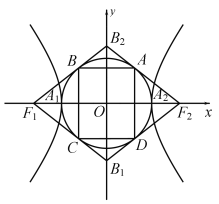
（1）雙曲線的離心率
______；
（2）菱形的面積
與矩形
的面積
的比值
______.
科目：高中數學 來源： 題型：
【題目】某公司對旗下的甲、乙兩個門店在1至9月份的營業額（單位：萬元）進行統計并得到如圖折線圖.
下面關于兩個門店營業額的分析中，錯誤的是( )
A.甲門店的營業額折線圖具有較好的對稱性，故而營業額的平均值約為32萬元
B.根據甲門店的營業額折線圖可知，該門店營業額的平均值在[20，25]內
C.根據乙門店的營業額折線圖可知，其營業額總體是上升趨勢
D.乙門店在這9個月份中的營業額的極差為25萬元
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，曲線C1的參數方程為
（
為參數），以坐標原點O為極點，x軸正半軸為極軸建立極坐標系，曲線C2的極坐標方程為
．
（1）寫出曲線C1和C2的直角坐標方程；
（2）已知P為曲線C2上的動點，過點P作曲線C1的切線，切點為A，求|PA|的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，已知
為橢圓
的上頂點，P為橢圓E上異于上、下頂點的一個動點．當點P的橫坐標為
時，
．
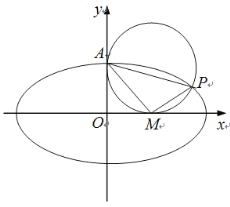
（1）求橢圓E的標準方程；
（2）設M為x軸的正半軸上的一個動點．
①若點P在第一象限內，且以AP為直徑的圓恰好與x軸相切于點M，求AP的長．
②若
，是否存在點N，滿足
，且AN的中點恰好在橢圓E上？若存在，求點N的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】天干地支紀年法，源于中國.中國自古便有十天干與十二地支.十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸，十二地支即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支紀年法是按順序以一個天干和一個地支相配，排列起來，天干在前，地支在后，天干由“甲”起，地支由“子”起，比如說第一年為“甲子”，第二年為“乙丑”，第三年為“丙寅”… …依此類推，排列到“癸酉”后，天干回到“甲”重新開始，即“甲戌”“乙亥”，之后地支回到“子”重新開始，即“丙子”… …依此類推.1911年中國爆發推翻清朝專制帝制、建立共和政體的全國性革命,這一年是辛亥年，史稱“辛亥革命”.1949新中國成立，請推算新中國成立的年份為( )
A.己丑年B.己酉年
C.丙寅年D.甲寅年
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的焦點在
軸上.
（1）若橢圓
的焦距為1，求橢圓的方程；
（2）設
分別是橢圓的左、右焦點，
為橢圓上的第一象限內的點，直線
交
軸與點
，并且
，證明：當
變化時，點
在某定直線上.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一飲料店制作了一款新飲料，為了進行合理定價先進行試銷售，其單價
（元）與銷量
（杯）的相關數據如下表：
單價 | 8.5 | 9 | 9.5 | 10 | 10.5 |
銷量 | 120 | 110 | 90 | 70 | 60 |
（1）已知銷量與單價具有線性相關關系，求關于的線性回歸方程；
（2）若該款新飲料每杯的成本為8元，試銷售結束后，請利用（1）所求的線性回歸方程確定單價定為多少元時，銷售的利潤最大？（結果四舍五入保留到整數）
附：線性回歸方程
中斜率和截距最小二乗法估計計算公式：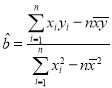
，
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】新冠肺炎期間某商場開通三種平臺銷售商品，收集一月內的數據如圖1；為了解消費者對各平臺銷售方式的滿意程度，該商場用分層抽樣的方法抽取4%的顧客進行滿意度調查，得到的數據如圖2．下列說法錯誤的是（ ）
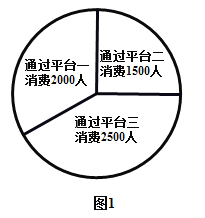
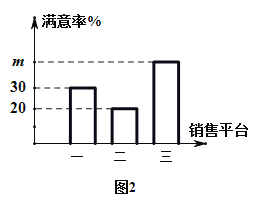
A.樣本容量為240
B.若樣本中對平臺三滿意的人數為40，則
C.總體中對平臺二滿意的消費者人數約為300
D.樣本中對平臺一滿意的人數為24人
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
