
【題目】執(zhí)行如圖所示的程序框圖,若輸出的 ![]() 值為11,則判斷框中的條件可以是( )
值為11,則判斷框中的條件可以是( )![]()
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】第1次執(zhí)行循環(huán)體, ![]() ,應(yīng)不滿足輸出的條件,n=2, 第2次執(zhí)行循環(huán)體,S=7,應(yīng)不滿足輸出的條件,n=3, 第3次執(zhí)行循環(huán)體,S=15,應(yīng)不滿足輸出的條件,n=4, 第4次執(zhí)行循環(huán)體,S=31,應(yīng)不滿足輸出的條件,n=5, 第5次執(zhí)行循環(huán)體,S=63,應(yīng)不滿足輸出的條件,n=6, 第6次執(zhí)行循環(huán)體,S=127,應(yīng)不滿足輸出的條件,n=7, 第7次執(zhí)行循環(huán)體,S=255,應(yīng)不滿足輸出的條件,n=8, 第8次執(zhí)行循環(huán)體,S=511,應(yīng)不滿足輸出的條件,n=9, 第9次執(zhí)行循環(huán)體,S=1023,應(yīng)不滿足輸出的條件,n=10, 第10次執(zhí)行循環(huán)體,S=2047,應(yīng)不滿足輸出的條件,n=11 第11次執(zhí)行循環(huán)體,S=4095,應(yīng)滿足輸出的條件, 故判斷框中的條件可以是S<4095?, 所以答案是:C
,應(yīng)不滿足輸出的條件,n=2, 第2次執(zhí)行循環(huán)體,S=7,應(yīng)不滿足輸出的條件,n=3, 第3次執(zhí)行循環(huán)體,S=15,應(yīng)不滿足輸出的條件,n=4, 第4次執(zhí)行循環(huán)體,S=31,應(yīng)不滿足輸出的條件,n=5, 第5次執(zhí)行循環(huán)體,S=63,應(yīng)不滿足輸出的條件,n=6, 第6次執(zhí)行循環(huán)體,S=127,應(yīng)不滿足輸出的條件,n=7, 第7次執(zhí)行循環(huán)體,S=255,應(yīng)不滿足輸出的條件,n=8, 第8次執(zhí)行循環(huán)體,S=511,應(yīng)不滿足輸出的條件,n=9, 第9次執(zhí)行循環(huán)體,S=1023,應(yīng)不滿足輸出的條件,n=10, 第10次執(zhí)行循環(huán)體,S=2047,應(yīng)不滿足輸出的條件,n=11 第11次執(zhí)行循環(huán)體,S=4095,應(yīng)滿足輸出的條件, 故判斷框中的條件可以是S<4095?, 所以答案是:C


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某城市收集并整理了該市2017年1月份至10月份各月最低氣溫與最高氣溫(單位; ![]() )的數(shù)據(jù),繪制了下面的折線圖。
)的數(shù)據(jù),繪制了下面的折線圖。
已知該市的各月最低氣溫與最高氣溫具有較好的線性關(guān)系,則根據(jù)該折線圖,下列結(jié)論錯誤的是( )
A.最低氣溫與最高氣溫為正相關(guān)
B.10月的最高氣溫不低于5月的最高氣溫
C.月溫差(最高氣溫減最低氣溫)的最大值出現(xiàn)在1月
D.最低氣溫低于 ![]() 的月份有4個
的月份有4個
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系中,以原點為極點, ![]() 軸的正半軸為極軸,以相同的長度單位建立極坐標(biāo)系,已知直線
軸的正半軸為極軸,以相同的長度單位建立極坐標(biāo)系,已知直線 ![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ![]() ,曲線
,曲線 ![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ![]() .
.
(1)設(shè) ![]() 為參數(shù),若
為參數(shù),若 ![]() ,求直線
,求直線 ![]() 的參數(shù)方程;
的參數(shù)方程;
(2)已知直線 ![]() 與曲線
與曲線 ![]() 交于
交于 ![]() ,設(shè)
,設(shè) ![]() ,且
,且 ![]() ,求實數(shù)
,求實數(shù) ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知下列命題:
①命題“ ![]() ,
, ![]() ”的否定是:“
”的否定是:“ ![]() ,
, ![]() ”;
”;
②若樣本數(shù)據(jù) ![]() 的平均值和方差分別為
的平均值和方差分別為 ![]() 和
和 ![]() 則數(shù)據(jù)
則數(shù)據(jù) ![]() 的平均值和標(biāo)準(zhǔn)差分別為
的平均值和標(biāo)準(zhǔn)差分別為 ![]() ,
, ![]() ;
;
③兩個事件不是互斥事件的必要不充分條件是兩個事件不是對立事件;
④在 ![]() 列聯(lián)表中,若比值
列聯(lián)表中,若比值 ![]() 與
與 ![]() 相差越大,則兩個分類變量有關(guān)系的可能性就越大.
相差越大,則兩個分類變量有關(guān)系的可能性就越大.
⑤已知 ![]() 為兩個平面,且
為兩個平面,且 ![]() ,
, ![]() 為直線.則命題:“若
為直線.則命題:“若 ![]() ,則
,則 ![]() ”的逆命題和否命題均為假命題.
”的逆命題和否命題均為假命題.
⑥設(shè)定點 ![]() 、
、 ![]() ,動點
,動點 ![]() 滿足條件
滿足條件 ![]() 為正常數(shù)),則
為正常數(shù)),則 ![]() 的軌跡是橢圓.其中真命題的個數(shù)為( )
的軌跡是橢圓.其中真命題的個數(shù)為( )
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系 ![]() 中,曲線
中,曲線 ![]() (
( ![]() 為參數(shù)且
為參數(shù)且 ![]() ),其中
),其中 ![]() ,在以
,在以 ![]() 為極點,
為極點, ![]() 軸正半軸為極軸的極坐標(biāo)系中,曲線
軸正半軸為極軸的極坐標(biāo)系中,曲線 ![]() .
.
(Ⅰ)求 ![]() 與
與 ![]() 交點的直角坐標(biāo);
交點的直角坐標(biāo);
(Ⅱ)若 ![]() 與
與 ![]() 相交于點
相交于點 ![]() ,
, ![]() 與
與 ![]() 相交于點
相交于點 ![]() ,求當(dāng)
,求當(dāng) ![]() 時
時 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若執(zhí)行右側(cè)的程序框圖,當(dāng)輸入的x的值為4時,輸出的y的值為2,則空白判斷框中的條件可能為( ) 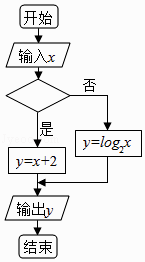
A.x>3
B.x>4
C.x≤4
D.x≤5
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù) ![]() 是定義域為
是定義域為 ![]() 的偶函數(shù),當(dāng)
的偶函數(shù),當(dāng) ![]() 時,
時, ![]() 若關(guān)于
若關(guān)于 ![]() 的方程
的方程 ![]()
![]() 有且僅有8個不同實數(shù)根,則實數(shù)
有且僅有8個不同實數(shù)根,則實數(shù) ![]() 的取
的取
值范圍是
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù) ![]() 是定義在
是定義在 ![]() 上的單調(diào)函數(shù),且對于任意正數(shù)
上的單調(diào)函數(shù),且對于任意正數(shù) ![]() 有
有 ![]() ,已知
,已知 ![]() ,若一個各項均為正數(shù)的數(shù)列
,若一個各項均為正數(shù)的數(shù)列 ![]() 滿足
滿足 ![]() ,其中
,其中 ![]() 是數(shù)列
是數(shù)列 ![]() 的前
的前 ![]() 項和,則數(shù)列
項和,則數(shù)列 ![]() 中第18項
中第18項 ![]() ( )
( )
A.![]()
B.9
C.18
D.36
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 各項均為正數(shù),
各項均為正數(shù), ![]() ,
, ![]() ,且
,且![]() 對任意
對任意![]() 恒成立,記
恒成立,記![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)證明:對任意正實數(shù)![]() ,
, ![]() 成等比數(shù)列;
成等比數(shù)列;
(3)是否存在正實數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 為等比數(shù)列.若存在,求出此時
為等比數(shù)列.若存在,求出此時![]() 和
和![]() 的表達式;若不存在,說明理由.
的表達式;若不存在,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com