
【題目】如圖所示,在直四棱柱![]() 中,
中,![]() ,點
,點![]() 是棱
是棱![]() 上一點.
上一點.

(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() ;
;
(3)試確定點![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() .
.
【答案】(1)見解析;(2)見解析;(3)點![]() 為棱
為棱![]() 的中點時,平面
的中點時,平面![]() 平面
平面![]() .
.
【解析】
(1)由題意可知,四邊形![]() 是平行四邊形,即
是平行四邊形,即![]() ,再根據線面平行的判定定理,證明即可.
,再根據線面平行的判定定理,證明即可.
(2)在直四棱柱![]() 中,
中,![]() 平面
平面![]() ,從而
,從而![]() ,由題意可知
,由題意可知![]() ,根據線面垂直的判定定理,證明
,根據線面垂直的判定定理,證明![]() 平面
平面![]() ,即可.
,即可.
(3)取![]() 的中點
的中點![]() ,
,![]() 的中點
的中點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .則
.則![]() 是
是![]() 的中點.由題意可知,
的中點.由題意可知,![]() ,根據面面垂直的性質定理,可知
,根據面面垂直的性質定理,可知![]() 平面
平面![]() ,當點
,當點![]() 為棱
為棱![]() 的中點時,
的中點時,![]() ,
,![]() 平面
平面![]() ,即可使得平面
,即可使得平面![]() 平面
平面![]() .
.
(1)因為![]() 為直四棱柱.
為直四棱柱.
所以![]() ,且
,且![]() .
.
所以四邊形![]() 是平行四邊形,即
是平行四邊形,即![]() .
.
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
(2)因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
又因為![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,所以
,所以![]() .
.
(3)當點![]() 為棱
為棱![]() 的中點時,平面
的中點時,平面![]() 平面
平面![]() .如圖,
.如圖,
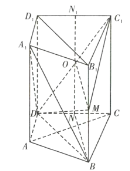
取![]() 的中點
的中點![]() ,
,![]() 的中點
的中點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
則![]() ,即
,即![]() 是
是![]() 的中點.
的中點.
因為![]() 是
是![]() 的中點,
的中點,![]() ,所以
,所以![]() .
.
因為在直四棱柱![]() 中
中
所以![]() 平面
平面![]()
又因為![]() 平面
平面![]()
所以平面![]() 平面
平面![]()
又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
當點![]() 為棱
為棱![]() 的中點時
的中點時
所以![]() ,且
,且![]() .
.
所以![]() 是平行四邊形,即
是平行四邊形,即![]() .
.
所以![]() 平面
平面![]() .
.
又因為![]() 平面
平面![]()
所以平面![]() 平面
平面![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐VABCD中,底面ABCD是矩形,VD⊥平面ABCD,過AD的平面分別與VB,VC交于點M,N.

(1) 求證:BC⊥平面VCD;
(2) 求證:AD∥MN.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐P—ABC中,PC![]() 底面ABC,AB=BC,D、F分別為AC、PC的中點,DE
底面ABC,AB=BC,D、F分別為AC、PC的中點,DE![]() AP于E。(1)求證:AP
AP于E。(1)求證:AP![]() 平面BDE;(2)求證:平面BDE
平面BDE;(2)求證:平面BDE![]() 平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱錐P—ABC所成上、下兩部分的體積比。
平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱錐P—ABC所成上、下兩部分的體積比。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】f(x),g(x)分別是定義在R上的奇函數和偶函數,當x<0時,f![]() (x)g(x)+f(x)g
(x)g(x)+f(x)g![]() (x)<0且f(﹣1)=0則不等式f(x)g(x)<0的解集為( )
(x)<0且f(﹣1)=0則不等式f(x)g(x)<0的解集為( )
A.(﹣1,0)∪(1,+∞)B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》卷第六《均輸》中,提到如下問題:“今有竹九節,下三節容量四升,上四節容量三升.問中間二節欲均容,各多少?”其大致意思是說,若九節竹每節的容量依次成等差數列,下三節容量四升,上四節容量三升,則中間兩節的容量各是( )
A.![]() 升、
升、![]() 升B.
升B.![]() 升、
升、![]() 升
升
C.![]() 升、
升、![]() 升D.
升D.![]() 升、
升、![]() 升
升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學成就的杰出代表作之一,其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積![]() (弦
(弦![]() 矢
矢![]() 矢
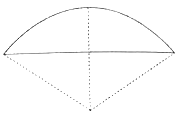
矢![]() ),弧田(如圖)由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角為
),弧田(如圖)由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角為![]() ,半徑等于6米的弧田,按照上述經驗公式計算所得弧田面積約為( )
,半徑等于6米的弧田,按照上述經驗公式計算所得弧田面積約為( )
A.12平方米B.16平方米C.20平方米D.24平方米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com