
【題目】已知函數f(x)=lnx,g(x)=x2 . (Ⅰ)求函數h(x)=f(x)﹣x+1的最大值;
(Ⅱ)對于任意x1 , x2∈(0,+∞),且x1<x2 , 是否存在實數m,使mg(x1)﹣mg(x2)﹣x2f(x2)+x1f(x1)恒為正數?若存在,求出m的取值范圍;若不存在,說明理由.
【答案】解:(Ⅰ)函數h(x)的定義域為(0,+∞), ∵h(x)=lnx﹣x+1,∴h′(x)= ![]() ﹣1=
﹣1= ![]() ,
,
當x∈(0,1)時,h′(x)>0;當x∈(1,+∞)時,h′(x)<0.
∴h(x)在(0,1)上是單調遞增,在(1,+∞)上單調遞減,
∴h(x)max=h(1)=0,即函數的最大值為0.
(Ⅱ)若mg(x2)﹣mg(x1)﹣x1f(x1)+x2f(x2)>0恒成立,只需mg(x2)+x2f(x2)>mg(x1)+x1f(x1),
設φ(x)=mg(x)+xf(x)=mx2+xlnx,
又0<x1<x2 , 則只需φ(x)在(0,+∞)上單調遞減.
∴φ′(x)=2mx+1+lnx≤0在(0,+∞)上成立,得2m≤ ![]() ,
,
設t(x)= ![]() ,則t′(x)=
,則t′(x)= ![]() ,知函數t(x)在(0,1)上單調遞減,在(1,+∞)上單調遞增,即t(x)min=t(1)=﹣1.
,知函數t(x)在(0,1)上單調遞減,在(1,+∞)上單調遞增,即t(x)min=t(1)=﹣1.
∴存在實數m≤﹣ ![]() ,使mg(x2)﹣mg(x1)﹣x1f(x1)+x2f(x2)恒為正數
,使mg(x2)﹣mg(x1)﹣x1f(x1)+x2f(x2)恒為正數
【解析】(Ⅰ)求出函數的定義域、導數h′(x),由導數的符號可知函數單調性,根據單調性即可得到最大值;(Ⅱ)mg(x2)﹣mg(x1)﹣x1f(x1)+x2f(x2)>0恒成立,只需mg(x2)+x2f(x2)>mg(x1)+x1f(x1),設φ(x)=mg(x)+xf(x)=mx2+xlnx,又0<x1<x2 , 則只需φ(x)在(0,+∞)上單調遞減.從而有φ′(x)=2mx+1+lnx≤0在(0,+∞)上恒成立,分離出參數m后化為函數最值即可,利用導數可求得函數的最值.
【考點精析】根據題目的已知條件,利用利用導數研究函數的單調性和函數的最大(小)值與導數的相關知識可以得到問題的答案,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數學 來源: 題型:
【題目】在△ABC中,角A、B、C所對的邊分別為a,b,c,cos2C+2 ![]() cosC+2=0.
cosC+2=0.
(1)求角C的大小;
(2)若b= ![]() a,△ABC的面積為
a,△ABC的面積為 ![]() sinAsinB,求sinA及c的值.
sinAsinB,求sinA及c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知非空集合A,B滿足以下兩個條件.
(ⅰ)A∪B={1,2,3,4,5,6},A∩B=;
(ⅱ)A的元素個數不是A中的元素,B的元素個數不是B中的元素,則有序集合對(A,B)的個數為( )
A.10
B.12
C.14
D.16
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD. 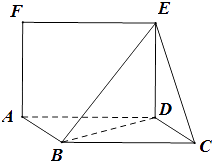
(Ⅰ)求證:BD⊥平面ECD.
(Ⅱ)求D點到面CEB的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列說法: ①函數y=﹣cos2x的最小正周期是π;
②終邊在y軸上的角的集合是{α|α= ![]() ,k∈Z};
,k∈Z};
③在同一直角坐標系中,函數y=sinx的圖象和函數y=x的圖象有三個公共點;
④函數f(x)=4sin(2x+ ![]() )(x∈R)可以改寫為y=4cos(2x﹣
)(x∈R)可以改寫為y=4cos(2x﹣ ![]() );
);
⑤函數y=sin(x﹣ ![]() )在[0,π]上是減函數.
)在[0,π]上是減函數.
其中,正確的說法是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 為奇函數.
為奇函數.
(1)若函數f(x)在區間 ![]() 上為單調函數,求m的取值范圍;
上為單調函數,求m的取值范圍;
(2)若函數f(x)在區間[1,k]上的最小值為3k,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com