
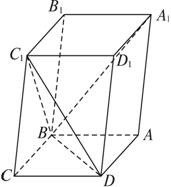
(1)求證:CC1⊥BD;
(2)當![]() 的值為多少時,能使A1C⊥平面C1BD?并加以證明.
的值為多少時,能使A1C⊥平面C1BD?并加以證明.
思路解析:在平行六面體中,通常以同一頂點上三條棱所在的直線的方向向量為基向量,建立空間向量基底.
(1)證明:取![]() =a,
=a,![]() =b,
=b,![]() =c為空間的一個基底,設菱形的邊長為a.
=c為空間的一個基底,設菱形的邊長為a.
∵![]() =a-b,∴
=a-b,∴![]() ·
·![]() =c·a-c·b=|c||a|cos〈c,a〉-|c||b|cos〈c,b〉=|c|acos60°-|c|acos60°=0.
=c·a-c·b=|c||a|cos〈c,a〉-|c||b|cos〈c,b〉=|c|acos60°-|c|acos60°=0.
∴![]() ⊥
⊥![]() .∴
.∴![]() ⊥
⊥![]() .
.
(2)設![]() =λ(λ>0),即|
=λ(λ>0),即|![]() |=λ|
|=λ|![]() |時,能使A
|時,能使A
∵C1D![]() 平面BC1D,BD
平面BC1D,BD![]() 平面BC1D,∴A
平面BC1D,∴A
∴![]() ·
·![]() =0且
=0且![]() ·
·![]() =0.
=0.
∵![]() =-(a+b+c),
=-(a+b+c), ![]() =a-c,〈a,b〉=〈b,c〉=60°,|a|=|b|=a,
=a-c,〈a,b〉=〈b,c〉=60°,|a|=|b|=a,
∴![]() ·
·![]() =-(a+b+c)·(a-c)=-a2-aacos60°+a·
=-(a+b+c)·(a-c)=-a2-aacos60°+a·![]() cos60°+
cos60°+![]()
∴3λ2-λ-2=0.∵λ>0,∴λ=1.
當λ=1時,
![]() ·
·![]() =-(a+b+c)·(a-b)=-a2+a2-aacos60°+aacos60°=0,
=-(a+b+c)·(a-b)=-a2+a2-aacos60°+aacos60°=0,
∴![]() ⊥
⊥![]() .∴A
.∴A
同理,當λ=1時,![]() ⊥
⊥![]() ,即A
,即A
由上述證明過程知當![]() 時,能使A
時,能使A
方法歸納 向量法解決線面垂直問題時,通常轉化為此直線的方向向量垂直于平面內兩不共線的向量問題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
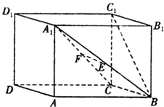 如圖所示,已知直平行六面體ABCD-A1B1C1D1的底面邊長均為2a,側棱長為a,∠ABC=60°,E、F分別是A1B、A1C的中點.
如圖所示,已知直平行六面體ABCD-A1B1C1D1的底面邊長均為2a,側棱長為a,∠ABC=60°,E、F分別是A1B、A1C的中點.查看答案和解析>>
科目:高中數學 來源:高考零距離 二輪沖刺優化講練 數學 題型:044
| |||||||||||
查看答案和解析>>
科目:高中數學 來源:單元雙測 同步達標活頁試卷 高二數學(下A) 人教版 題型:047
| |||||||||||||||
查看答案和解析>>
科目:高中數學 來源:同步題 題型:證明題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com