設數列{bn}(n∈N*)的前n項和為Sn,點(Sn,bn)恒在函數f(x)=-2x+2的圖象上;數列{an}(n∈N*)為等差數列,且a3=8,a7=20.
(1)求數列{an}的通項公式;
(2)求數列{bn}的通項公式;
【答案】
分析:(1)先根據a
3=8,a
7=20求得公差,進而根據等差數列通項公式求得首項,則數列{a
n}的通項公式可得.
(2)把b
n=S
n-S
n-1代入-2S
n+2=b
n,整理得3(S
n-1)=S
n-1-1判斷出數列{S
n-1}是以

為公比的等比數列,首項是S
1,則數列{S
n-1}通項公式可得,進而求得S
n,最后根據-2S
n+2=b
n,求得求數列{b
n}的通項公式;
解答:解:(1)d=
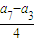
=3
∴a
3=a
1+2d=8,a
1=2
∴a
n=2+(n-1)×3=3n-1
(2)依題意可知-2S
n+2=b
n,
2b
1+2=b
1,b
1=-2
∵當n≥2時,b
n=S
n-S
n-1,
∴-2S
n+2=S
n-S
n-1,整理得3(S
n-1)=S
n-1-1
數列{S
n-1}是以

為公比的等比數列,首項是S
1∴S
n-1=(-3)×(

)
n-1=-(

)
n-2
∴S
n=-(

)
n-2+1
∴b
n=2•(

)
n-2點評:本題主要考查了用數列遞推式求數列通項公式的問題.考查了學生對數列問題的綜合掌握.

 為公比的等比數列,首項是S1,則數列{Sn-1}通項公式可得,進而求得Sn,最后根據-2Sn+2=bn,求得求數列{bn}的通項公式;
為公比的等比數列,首項是S1,則數列{Sn-1}通項公式可得,進而求得Sn,最后根據-2Sn+2=bn,求得求數列{bn}的通項公式;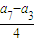 =3
=3 為公比的等比數列,首項是S1
為公比的等比數列,首項是S1 )n-1=-(
)n-1=-( )n-2
)n-2 )n-2+1
)n-2+1 )n-2
)n-2

 閱讀快車系列答案
閱讀快車系列答案