
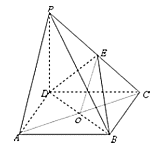
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC,E是PC的中點,

(1)證明:PA∥平面EDB
(2)證明:平面BDE![]() 平面PCB
平面PCB
【答案】(1)見解析;(2)見解析
【解析】試題分析:(1)取BD中點O,由三角形中位線性質得OE//PA,再根據線面平行判定定理得結論,(2)先根據等腰三角形性質得DE垂直PC,再根據PD垂直平面ABCD得平面PDC垂直平面ABCD,再根據ABCD是正方形得CD垂直BC,因此由面面垂直性質定理得BC垂直平面PCD,即BC垂直DE,最后根據線面垂直判定定理得DE垂直平面PBC,即得平面BDE![]() 平面PCB.
平面PCB.
試題解析:(1)取BD中點O,則OE//PA,所以PA//平面EDB
(2)由條件得PD垂直EDB,所以PD垂直BC,又CD垂直BC,所以BC垂直PCD,即BC垂直DE,又DE垂直PC,所以DE垂直平面PBC,即平面BDE![]() 平面PCB.
平面PCB.
點睛:垂直、平行關系證明中應用轉化與化歸思想的常見類型.
(1)證明線面、面面平行,需轉化為證明線線平行.
(2)證明線面垂直,需轉化為證明線線垂直.
(3)證明線線垂直,需轉化為證明線面垂直.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ax+b , g(x)=ex(cx+d),若曲線y=f(x)和曲線y=g(x)都過點P(0,2),且在點P處有相同的切線y=4x+2.
(1)求a , b , c , d的值;
(2)若x≥-2時,恒有f(x)≤kg(x),求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2015﹣2016賽季CBA聯賽中,某隊甲、乙兩名球員在前10場比賽中投籃命中情況統計如下表(注:表中分數 ![]() ,N表示投籃次數,n表示命中次數),假設各場比賽相互獨立.
,N表示投籃次數,n表示命中次數),假設各場比賽相互獨立.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
根據統計表的信息:
(1)從上述比賽中等可能隨機選擇一場,求甲球員在該場比賽中投籃命中率大于0.5的概率;
(2)試估計甲、乙兩名運動員在下一場比賽中恰有一人命中率超過0.5的概率;
(3)在接下來的3場比賽中,用X表示這3場比賽中乙球員命中率超過0.5的場次,試寫出X的分布列,并求X的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知長方形 ![]() ,
, ![]() ,
, ![]() ,以
,以 ![]() 的中點
的中點 ![]() 為原點,建立如圖所示的平面直角坐標系
為原點,建立如圖所示的平面直角坐標系 ![]() .
.
(1)求以 ![]() 為焦點,且過
為焦點,且過 ![]() 兩點的橢圓的標準方程;
兩點的橢圓的標準方程;
(2)在(1)的條件下,過點 ![]() 作直線
作直線 ![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點 ![]() ,設
,設 ![]() ,點
,點 ![]() 坐標為
坐標為 ![]() ,若
,若 ![]() ,求
,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以坐標原點 ![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.已知點
軸的非負半軸為極軸建立極坐標系.已知點 ![]() 的極坐標為
的極坐標為 ![]() ,曲線
,曲線 ![]() 的參數方程為
的參數方程為 ![]() 為參數).
為參數).
(1)直線 ![]() 過
過 ![]() 且與曲線
且與曲線 ![]() 相切,求直線
相切,求直線 ![]() 的極坐標方程;
的極坐標方程;
(2)點 ![]() 與點
與點 ![]() 關于
關于 ![]() 軸對稱,求曲線
軸對稱,求曲線 ![]() 上的點到點
上的點到點 ![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC,E是PC的中點,
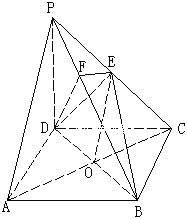
(1)證明:PA∥平面EDB
(2)證明:平面BDE![]() 平面PCB
平面PCB
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,|AB|=4,|AD|=2,O為AB中點,P,Q分別是AD和CD上的點,且滿足① ![]() =
= ![]() ,②直線AQ與BP的交點在橢圓E:
,②直線AQ與BP的交點在橢圓E: ![]() +
+ ![]() =1(a>b>0)上.
=1(a>b>0)上.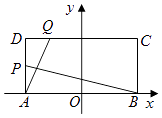
(Ⅰ)求橢圓E的方程;
(Ⅱ)設R為橢圓E的右頂點,M為橢圓E第一象限部分上一點,作MN垂直于y軸,垂足為N,求梯形ORMN面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com