定義在R+上的函數f(x)滿足:
(1)存在a>1,使f(a)≠0;
(2)對任意的實數b,有f(xb)=bf(x).若方程f(mx)•f(mx2)=4f2(a)的所有解大于1,求m的取值范圍.
【答案】
分析:令t=x
b,則b=log
xt,可得log
xt=
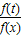
,進而根據方程f(mx)•f(mx
2)=4f
2(a)的所有解大于1,我們可以得到2log
a2x+3log
am•log
ax+log
a2m-4=0的所有解大于1,令u=log
ax,則u
2x+3log
am•u+log
a2m-4=0的所有解大于0,結合韋達定理,可以構造一個關于m的不等式組,解不等式組,即可得到答案.
解答:解:令t=x
b,則b=log
xt,
則f(t)=log
xt•f(x)
即log
xt=
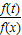
若f(mx)•f(mx
2)=4f
2(a)的所有解大于1,
則
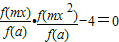
的所有解大于1,
即log
a(mx)•log
a(mx
2)-4=0的所有解大于1,
即2log
a2x+3log
am•log
ax+log
a2m-4=0的所有解大于1,
令u=log
ax,由a>1,
則u
2x+3log
am•u+log
a2m-4=0的所有解大于0
由韋達定理可得
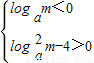
解得:0<m≤
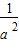
故m的取值范圍為(0,
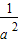
]
點評:本題考查的知識點是函數與議程的綜合應用,抽象函數的應用,其中根據已知條件,得到log
xt=
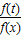
,從而將抽象問題具體化,是解答本題的關鍵.

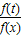 ,進而根據方程f(mx)•f(mx2)=4f2(a)的所有解大于1,我們可以得到2loga2x+3logam•logax+loga2m-4=0的所有解大于1,令u=logax,則u2x+3logam•u+loga2m-4=0的所有解大于0,結合韋達定理,可以構造一個關于m的不等式組,解不等式組,即可得到答案.
,進而根據方程f(mx)•f(mx2)=4f2(a)的所有解大于1,我們可以得到2loga2x+3logam•logax+loga2m-4=0的所有解大于1,令u=logax,則u2x+3logam•u+loga2m-4=0的所有解大于0,結合韋達定理,可以構造一個關于m的不等式組,解不等式組,即可得到答案.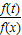
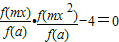 的所有解大于1,
的所有解大于1,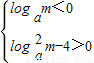
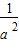
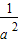 ]
]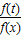 ,從而將抽象問題具體化,是解答本題的關鍵.
,從而將抽象問題具體化,是解答本題的關鍵. 

 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案