
分析 (I)先求出h(x)的定義域是否對稱,再計算h(-x)并化簡,觀察h(-x)和h(x)的關系得出結論;
(II)根據f(x)=log3[g(x)]得$\frac{x-1}{x+1}=-2ax+a+1$,化簡為2ax2+ax-a-2=0,討論a是否為0得出x2+$\frac{1}{2}$x-$\frac{1}{a}$-$\frac{1}{2}$=0,利用二次函數的性質得出a的范圍.
解答 解:(I)證明:a=-1時,h(x)=log3$\frac{x-1}{x+1}$+2x,
由函數有意義得$\frac{x-1}{x+1}$>0,解得x<-1或x>1.
∴h(x)的定義域為(-∞,-1)∪(1,+∞),關于原點對稱.
∵h(-x)=log3$\frac{-x-1}{-x+1}$-2x=log3$\frac{x+1}{x-1}$-2x=-h(x),
∴h(x)為奇函數.
(II)由f(x)=log3g(x)可得$\frac{x-1}{x+1}=-2ax+a+1$,
化簡得,2ax2+ax-a-2=0,①
顯然,當a=0時,方程①無解,不符合題意;
∴a≠0,由①得2a(x2+$\frac{1}{2}$x-$\frac{1}{a}$-$\frac{1}{2}$)=0
令F(x)=x2+$\frac{1}{2}$x-$\frac{1}{a}$-$\frac{1}{2}$,則F(x)=x2+$\frac{1}{2}$x-$\frac{1}{a}$-$\frac{1}{2}$在(-∞,-1)∪(1,+∞)內有兩個零點,
∴$\left\{\begin{array}{l}{F(-1)<0}\\{F(1)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{-\frac{1}{a}<0}\\{1-\frac{1}{a}<0}\end{array}\right.$,解得0<a<1.
∴a的取值范圍是(0,1).
點評 本題考查了函數奇偶性的判斷,函數零點的個數判斷與函數圖象的關系,二次函數的性質,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
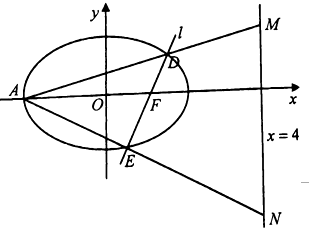 已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,短軸長為2$\sqrt{3}$,點P為橢圓C上一點,且點P到點F的最遠距離是最近距離的3倍.
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,短軸長為2$\sqrt{3}$,點P為橢圓C上一點,且點P到點F的最遠距離是最近距離的3倍.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | 2 | C. | 4 | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
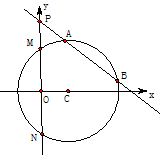 已知圓心在x軸正半軸上的圓C與直線5x+12y+21=0相切,與y軸交于M,N兩點,且∠MCN=120°.
已知圓心在x軸正半軸上的圓C與直線5x+12y+21=0相切,與y軸交于M,N兩點,且∠MCN=120°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com